강체가 있는 단순보의 처짐 (구독자 질의)
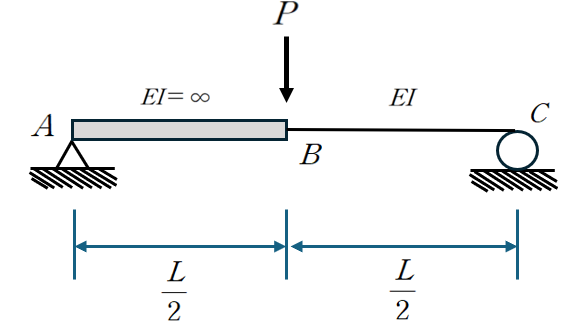
1.개요
한 구독자 분께서
“EI 강체(EI → ∞)가 오히려 문제를 더 쉽게 만든다”는 제 의견에 대해 깊은 인상을 받으셨다고 하며,
여러 가지 EI 강체가 포함된 문제들을 직접 시도해 보신 후 위 문제에 대해 질문을 주셨습니다.
해당 구독자 분은 역학 자체에 흥미가 있고기존 풀이와는 다른 접근법을 탐구하는 데 관심이 많으며
현재 서울시 7급을 준비 중인 수험생이라고 밝혀 주셨습니다.
이번 글에서는 그분의 질문을 바탕으로,
위 구조물을 변위법의 관점에서 해석하여 B점의 수직 처짐을 구하는 과정을 살펴보겠습니다.
조금 개념적인 이야기가 될 수 있지만, 핵심은 다음과 같습니다.
위 구조물은 C점의 회전 자유도를 무시할 수 있는 조건(EI 강체) 이 주어져 있으므로,
이를 통해 수정된 강성도(modified stiffness) 를 적용할 수 있습니다.
이 경우 구조물은 다음과 같은 특징을 갖습니다.
- C점의 회전 자유도는 제거된다
- 결과적으로 B점의 수직 처짐이 유일한 자유도(1 DOF) 가 된다
- 즉, B점의 처짐 하나만 알면 구조물 전체의 변형 상태를 모두 표현할 수 있다
다시 말해,
이 문제는 겉보기와 달리 다자유도 문제가 아니라
단자유도 문제로 축약될 수 있는 구조물입니다.
이제 이 관점에서 두 가지 대표적인 해석 방법을 비교해 보겠습니다.
- 응력법의 대표: 카스틸리아노 정리
- 변위법의 대표: 처짐각법(Slope Deflection Method)
같은 문제를
- 에너지 관점에서 어떻게 해석할 수 있는지,
- 그리고 변위 기반 관계식으로는 얼마나 직관적으로 정리되는지를
차례대로 살펴보도록 하겠습니다.
이를 통해
EI 강체가 단순히 “제약 조건”이 아니라, 문제를 단자유도로 환원시켜 계산을 획기적으로 단순화하는 장치라는 점을 명확히 느끼실 수 있을 것이라 생각합니다.
2. 문제풀이 Ⅰ (카스틸리아노 법칙)
우선 A와 C의 반력은 각각 P/2입니다. AB부분은 강체이므로 변형에너지가 0이 됩니다.
반면에 BC 부분은 휨변형으로 인한 변형에너지가 존재합니다.
따라서 c 점에서 x만큼 거리가 있는점에서의 자유물체도를 그려보면 다음과 같습니다.

따라서 휨에 의한 변형에너지는 다음과 같습니다.

카스틸리아노 2법칙을 적용하여 휨에너지를 하중 P에 대해 미분하면 처짐값이 산정됩니다.
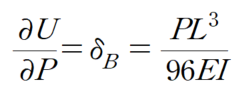
2. 문제풀이 Ⅱ (처짐각법)
B점의 수직변위 δB가 발생시 강체AB와 와 EI부재 BC의 적합조건은 다음과 같습니다.
EI가 ∞ 인 곳은 회전각이0이므로 인접한 부분도 회전각이 0이어야 한다
따라서 AB 부재에 현회전각이 생기면 B부분의 회전각을 0을 유지하기 위해 AB의 회전각만큼 추가 회전이 이뤄져서 변형도는 아래와 같게 됩니다.

즉, B는 강체와의 적합조건을 만족하기 위해 2×δB/L 만큼 회전하고, BC와의 현회전각반큼 추가로 생기게 됩니다.
따라서 위의 변위도에 가상 변위의 법칙을 적용하게 되면 다음과 같은 방정식이 성립하게 됩니다.
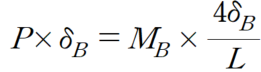
한편 B지점의 모멘트는 수정된 강성도에 따라 다음과 같이 표현할 수 있습니다.

이를 가상변위의 법칙에 대입하면 다음과 같습니다.

따라서 이를 δB에 대해 산정하면

3. 마무리하며
서로 완전히 다른 접근법을 사용하였지만,
하나는 적분을 기반으로 한 에너지 해석이었고
다른 하나는 구조물을 하나의 자유도로 환원하여 스프링으로 치환하듯 매우 직관적으로 푸는 방식이었습니다.
풀이 과정은 전혀 달랐지만, 최종 결과는 정확히 일치하였습니다.
이 점이 시사하는 바는 분명합니다.
문제에 EI가 무한대인 강체 부재가 등장한다면,
이는 전형적인 재료역학 문제의 틀에서 벗어나는 요소일 수는 있지만
결코 문제를 어렵게 만들기 위한 장치가 아니라
오히려 수험생이 구조를 단순화하여 더 쉽게 풀 수 있도록 유도하는 출제자의 힌트라고 볼 수 있습니다.
만약 “강체(EI → ∞)가 포함되었는데 풀이가 오히려 더 복잡해졌다”라고 느껴진다면,
그때는 계산을 밀어붙일 것이 아니라
풀이의 관점 자체를 재조정해야 할 신호라고 생각하셔야 합니다.
대부분의 경우, 더 간단한 자유도 설정이나 구조적 치환을 통해
훨씬 효율적인 해법으로 갈아탈 수 있습니다.
올해 시험에 강체 문제가 출제될지 여부는 알 수 없지만,
이번 풀이에서 보여드린 사고 과정을 하나의 기준으로 삼아
비슷한 문제가 등장했을 때
“어떻게 하면 더 단순한 구조로 볼 수 있을까?”를 한 번 더 고민해 보신다면
실전에서 분명 큰 도움이 될 것이라 생각합니다.
강체는 위협이 아니라 기회가 될 수 있습니다.
그 관점을 익히는 것이 이번 풀이의 가장 중요한 메시지입니다.