2017년 응용역학 가형 20번

B지점 수직반력, 영향선으로 한 줄에 끝내기

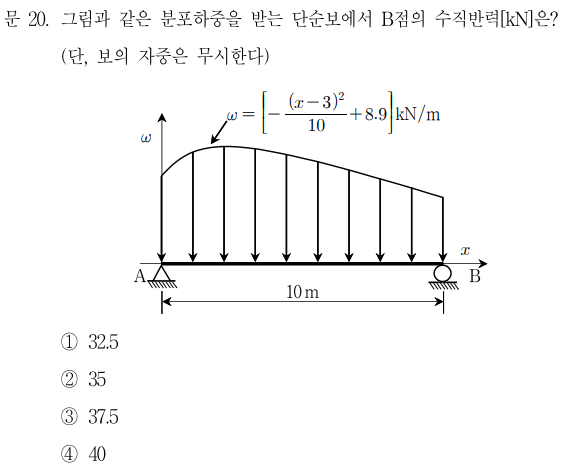
문제:
길이 10 m 단순보에 다음과 같은 분포하중이 작용한다.
$$
\omega(x) = -\frac{(x-3)^2}{10} + 8.9 ;[\mathrm{kN/m}]
$$
이때 B지점 수직반력 ( R_B )을 구하여라.
(단, 보의 자중은 무시한다.)

---

1. 뮬러–브레슬라우로 영향선 그리기

구하고 싶은 값은 B지점의 수직반력 ( R_B ) 이므로
B지점의 지지력을 제거하고 위로 단위변위 ( +1 ) 을 주면 그때의 변형형상이 영향선이다.
단순보의 영향선은 선형이므로
$$
y_{\mathrm{IL}}(x) = \frac{x}{L} = \frac{x}{10}, \qquad (0 \le x \le 10)
$$
가상변위의 법칙(virtual work principle)에 따라,
$$
R_B = \int_0^L \omega(x) , y_{\mathrm{IL}}(x) , dx
$$
따라서
$$
R_B = \int_{0}^{10} \omega(x) \frac{x}{10} , dx
= \frac{1}{10} \int_{0}^{10} x \left( -\frac{(x-3)^2}{10} + 8.9 \right) dx
$$

---

2. 적분 전개

먼저,
$$ (x-3)^2 = x^2 - 6x + 9 $$
이므로
$$
x(x-3)^2 = x^3 - 6x^2 + 9x
$$
대입하면
$$
R_{B} = \frac{1}{10} \left[
-\frac{1}{10} \int_0^{10} (x^3 - 6x^2 + 9x) , dx+8.9 \int_0^{10} x , dx
\right]
$$
각 항을 적분하면,
$$
\int_0^{10} (x^3 - 6x^2 + 9x) , dx
= \left[ \frac{x^4}{4} - 2x^3 + \frac{9}{2}x^2 \right]_0^{10}
= 2500 - 2000 + 450 = 950
$$
$$
\int_0^{10} x , dx = \left[ \frac{x^2}{2} \right]_0^{10} = 50
$$
따라서
$$
R_B = \frac{1}{10} \left( -\frac{1}{10} \times 950 + 8.9 \times 50 \right)
= \frac{1}{10} \left( -95 + 445 \right)
= \frac{350}{10} = 35 ;[\mathrm{kN}]
$$

---

3. 정답

$$
\boxed{R_B = 35;\mathrm{kN}}
$$

---