2017년 7급 국가직 응용역학 4번 풀이 (힘의 평형과 가상변위의 법칙)

2017년 7급 국가직 응용역학 4번

1. 개요

힘의 평형과 가상변위의 법칙

2017년 7급 국가직 응용역학 문제들 중에는 힘의 평형을 이용해 풀이하는 유형들이 여럿 있습니다.
하지만 이들 대부분은 가상변위의 법칙을 적용해도 똑같이, 오히려 더 쉽게 풀 수 있습니다.

그렇다고 해서 “가상변위로 풀면 더 쉬운 문제”가 따로 있는 것은 아닙니다.
두 방법은 결국 같은 원리에 기반하므로, 가상변위로 유도한 공식과 힘의 평형으로 유도한 공식은 동일한 결과를 줍니다.

 

A 매트릭스와 Kinematic 관계 (변위 매트릭스를 공부하는 사람을 위해)

이 원리는 구조기술사 수험생들이 흔히 말하는 ‘A 매트릭스’를 힘의 평형으로 세우는 이유와도 같습니다.
즉, Kinematic 관계(운동학적 관계) 를 직접 세우기 어렵다면, 평형방정식을 통해 동일한 관계를 얻을 수 있다는 뜻입니다.

 

왜 가상변위의 법칙을 선호하는가

평형방정식보다 가상변위의 법칙을 선호하는 이유는 명확합니다.
가상변위를 이용하면

• 필요한 식의 개수가 줄어들고,
• 구조물의 자유도(Degree of Freedom) 와 직접적으로 연관되며,
• 문제를 더 직관적으로 이해할 수 있기 때문입니다.

힘의 평형방정식은 물론 역학의 기본입니다.
하지만 그 위에서 한 단계 더 깊은 이해를 쌓고 싶다면 가상변위의 법칙을 적극적으로 활용해보길 권합니다.

 

2. 문제의 핵심 포인트

케이블에 작용하는 힘의 관계

이 문제에서는 케이블의 응력(stress) 이 탄성받침의 응력과 같아야 합니다.
그런데 케이블의 단면적이 탄성받침 단면적의 절반이므로,
두 부재에 걸리는 힘(force) 의 크기는 다음 관계로 해석할 수 있습니다.

따라서 단면적이 절반이라면,
케이블이 받는 힘은 C점 반력의 절반이 됩니다.

즉,

케이블의 단면적이 작을수록 같은 응력을 유지하기 위해
케이블이 분담하는 힘의 크기는 작아진다.

따라서 외력 3 kN은 케이블과 반력이 1 : 2의 비율로 분담해야 합니다.
즉, 케이블이 1 kN, 탄성받침(또는 반력)이 2 kN을 각각 부담하게 됩니다.

외력을 3 kN으로 설정한 것은 단순한 수치가 아니라,
계산을 쉽게 하도록 한 출제자의 배려로 볼 수 있습니다.
복잡한 비례식을 세우지 않고도
힘의 분담 관계를 직관적으로 파악할 수 있게 만든 것입니다.

3. 가상 변위의 법칙

쉬운 문제임을 알고 있습니다. 부디 답을 구한다는 느낌보다는 앞으로의 풀이가 평형방정식과 어떤 관계가 있는지 관찰하시면 좋을 것입니다,

아래 하중을 놓고 C 지점에 θ 만큼 가상 변위를 부여하겠습니다.

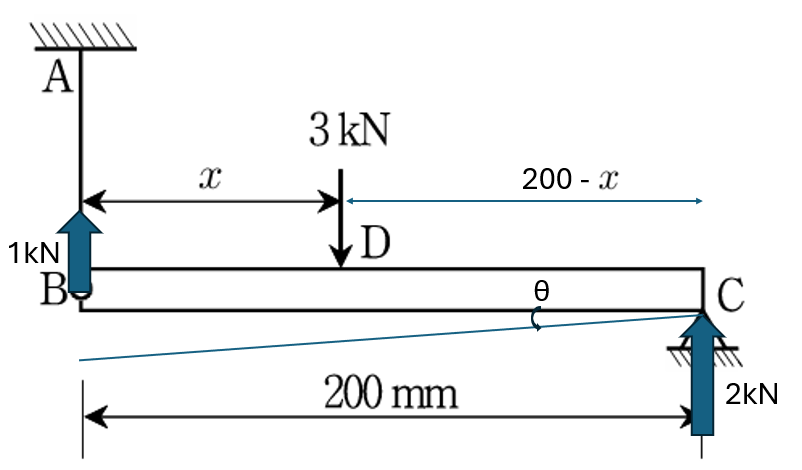
D점의 하중 3kN는 (200-x)×θ 만큼 이동하였으며

A점의 하중 1kN는 200 ×θ 만큼 이동하였습니다.

해당 가상변위로 인하여 외력 3kN로 안한 외부일은 내력 1kN가 한 내부일과 동일합니다.

이를 식으로 표현하겠습니다.

4. 평형방정식 

동일한 구조물 BDC 의 자유물체도를 통하여 C점에 대한 평형방정식을 세워보겠습니다.

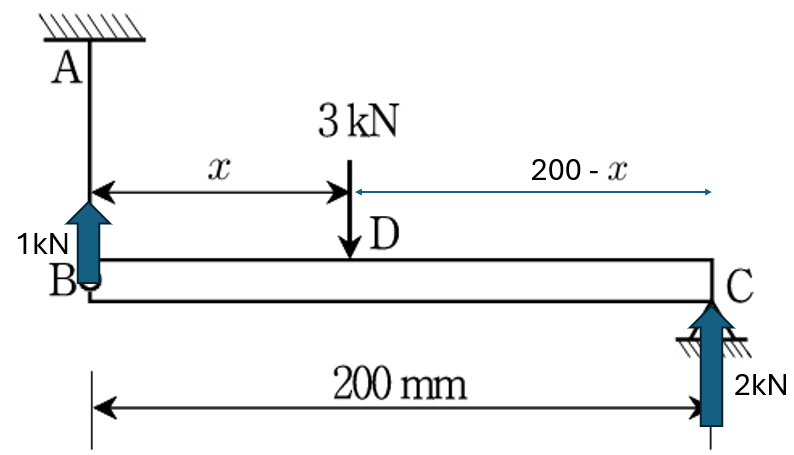
5. 마무리 하며

문제의 답은 방정식을 풀어보면

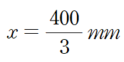
라는 답 (③번) 이 나옵니다.

하지만 진정으로 주목해야 할 부분은 정답 자체가 아닙니다.

이 간단한 문제 속에서도, 가상변위의 법칙을 이용해 유도한 식과 힘의 평형방정식으로부터 유도한 식이
완전히 동일한 형태로 나타납니다.

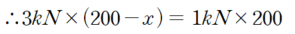
이 유도되었습니다.

즉, Kinematic 관계와 힘의 평형관계는 궁극적으로 동일한 결론의 식을 만들어 냅니다.

이를 통해 kinematic 과 힘의 평형은 동일한 결론에 다다르며 

한쪽을 산정하기 힘들면 나머지 한쪽을 산정하기 쉽다 라는 점도 깨달을 수 있습니다. 

 

즉,

Kinematic 관계(운동학적 접근) 와 힘의 평형 관계(정역학적 접근) 는
서로 다른 길을 통해 동일한 결론에 도달합니다.

 

이 사실을 이해하면,
한쪽 접근이 복잡하거나 막힐 때 다른 접근법으로 쉽게 해결할 수 있다는 자신감을 얻게 됩니다.

참고로, 2023년 7급 국가직 응용역학 17번 문제 또한 평형방정식과 가상변위의 법칙을 함께 비교해보면
두 접근이 얼마나 자연스럽게 연결되는지 확인할 수 있습니다.

https://oreostructure.tistory.com/32

2023년 7급 국가직 응용역학 풀이 (계산량은 최소화 하여 풀자)