2022년 9급 국가직 응용역학 개론 10번 - 보기를 통한 합리적 추론 기술

1. 개요

위의 문제를 보면,
“계산을 하지 않고 보기만 보고 바로 ①번을 선택할 수 있다”라고 하면선뜻 믿기 어려울 수도 있습니다.
하지만 실제 응용역학개론 문제를 자세히 살펴보면,보기의 구성을 분석하는 것만으로도
정답을 50%, 심지어 100% 확률로 추론할 수 있는 경우가 의외로 많습니다.
앞으로는 특히 9급 응용역학 문제를 중심으로,이러한 ‘보기 분석을 통한 합리적 추론법’ 에 대해서도
기회가 될 때마다 다뤄볼 예정입니다.
 

2. 문제풀이

이 문제를 정석적으로 풀자면 공액보법을 사용하는 것이 가장 편리합니다.
하지만 이는 삼각 분포하중의 단순보의 C지점에서 모멘트를 구한다는 점에서 긴시간이 소요됩니다.
다만, 시험장에서 시간을 절약하기 위해서는
대략적인 처짐의 범위를 암산 수준으로 판단할 수 있으면 좋습니다.

중앙점의 처짐을 δ 라고 하면 C점의 처짐은 δ/2 보다는 크고 δ보다는 작아야 합니다.
이때 δ는 다음과 같습니다.

따라서 δc 는 다음과 같이 표현 할 수 있습니다. 

좀더 명확하게 하기 위해 분모를 동일하게 할 필요가 있어 보입니다.

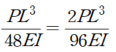
따라서

라고 표시할 수 있다. 즉, δc는 대략 PL^3/EI 를 제외 했을 때 대략 상수로는 1%~2% 정도의 값을 갖게 됩니다.
이제 PL^3/EI 를 제외하고 보기를 살펴보도록 합시다.

768의 1%는 7.68 입니다. 소숫점 두자리로 만들어 버리면 된다.
2%는 이의 두배이므로 대략 15~16 사이값이 됩니다.
1%에서 2% 사이를 충족하는 답은 보기 ① 밖에 없습니다
따라서 답은 ① 입니다.
 

3. 마무리하며

응용역학 시험에서는 시간에 쫓기거나, 아무리 해도 풀리지 않는 순간이 반드시 찾아옵니다.
그럴 때는 과감하게 문제를 포기하기보다,
합리적인 범위를 설정하여 추론 기반으로 찍는 연습이 필요합니다.
예를 들어 위의 풀이처럼,
분모를 기준으로 1%, 5%, 10% 수준의 수치 범위를 미리 감 잡아두면,
정확한 계산을 하지 않아도 답에 근접한 선택지를 충분히 찾아낼 수 있습니다.
이는 단순한 ‘운’이 아니라,
문제를 빠르게 분석해 가능한 값을 추정하는 능력,
즉 시험장에서의 판단력입니다.
객관식 시험에서는 다음의 말이 언제나 유효합니다.

“찍기도 실력이다.”