보 구조물 변위법의 기본 - 처짐각법 pt 1

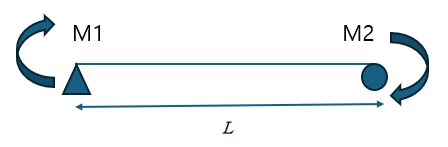
1. 개요

단순보 양끝에 모멘트가 작용하면 휨은 어떻게 될까요?
구조물을 스프링처럼 단순 모델로 치환하는 직관은 유용하지만, 보는 단자유도 스프링과 달리 양단 회전이 독립적으로 존재합니다. 다시 말해, 스프링은 인장/압축 하나의 작용만 고려하면 되지만, 보의 양단에는 서로 다른 방향(시계/반시계)의 모멘트 M1, M2가 동시에 작용할 수 있습니다.

이 글에서는 양단 모멘트 M1, M2를 받은 단순보에 대해, 각 단의 회전각(슬로프)과 처짐 관계를 공액보법(Conjugate Beam Method) 으로 간결하게 유도해볼 것 입니다.

 

2. 공액보법을 통한 유연도 유도

위 구조물의 경우 모멘트는 M1에서 -M2까지 선형적으로 변합니다. 이에 따른 곡률 (M/EI) 는 다음과 같이 나타낼 수 있습니다.

공액보법의 원리에 따라, 좌측 지점을 A, 우측 롤러 지점을 B라 하면 공액보에서 각 지점의 수직반력은 실제 보의 회전각(θ) 에 대응합니다. 따라서 M/EI 도를 실제 보에 작용하는 등가 하중 분포로 간주하고, 이 하중에 대한 공액보의 반력을 구하면
그 값이 곧 A, B 지점의 회전각을 의미하게 됩니다.

삼각 분포하중을 등가 하중으로 변환하여 단순화 하면 다음 그림과 같이 됩니다.

RA 반력을 B 지점에 대한 모멘트 평형으로 구해보면 다음과 같습니다. 

이를 정리해보면 RA는 다음과 같이 나타낼 수 있습니다. 

RB는 수직 힘에 대해 평형방정식을 세우면 다음과 같이 표현 됩니다. 

따라서 행렬식으로 표현하면 다음과 같이 표현 할 수 있습니다.

3. 역행렬을 통한 Stiffness 유도

따라서 식으로 풀어쓰면 다음과 같이 서술 할 수 있습니다.

4. 의미

이번에 유도한 식은 보 구조물의 양단 모멘트와 회전각 사이의 관계를 나타내는,매우 중요한 기본식입니다.

이 관계식은 단순히 보(Beam) 해석에만 국한되지 않습니다.
프레임(Frame) 구조물 해석에서도 핵심적으로 활용됩니다.

그 이유는 대부분의 구조물에서 축강성(Axial Stiffness) 이 휨강성(Flexural Stiffness) 보다 훨씬 크기 때문에,
일반적으로 축변형을 무시하고 휨변형만으로 전체 변형을 산정하기 때문입니다.

비록 식의 유도 과정은 다소 복잡해 보이지만,이 관계는 유연도(Flexibility) 와 강성도(Stiffness) 의 상호 관계를 설명하는
기초이자 핵심 개념이므로 꼭 기억해 두는 것이 좋습니다.

앞으로도 유연도법(삼연모멘트법) 과 강성도법(처짐각법) 을 이용하여이러한 기본 원리를 적용하면,
훨씬 많은 문제를 쉽고 체계적으로 풀 수 있을 것입니다.