2025년 5급 공채 응용역학 1번 문제
1. 개요
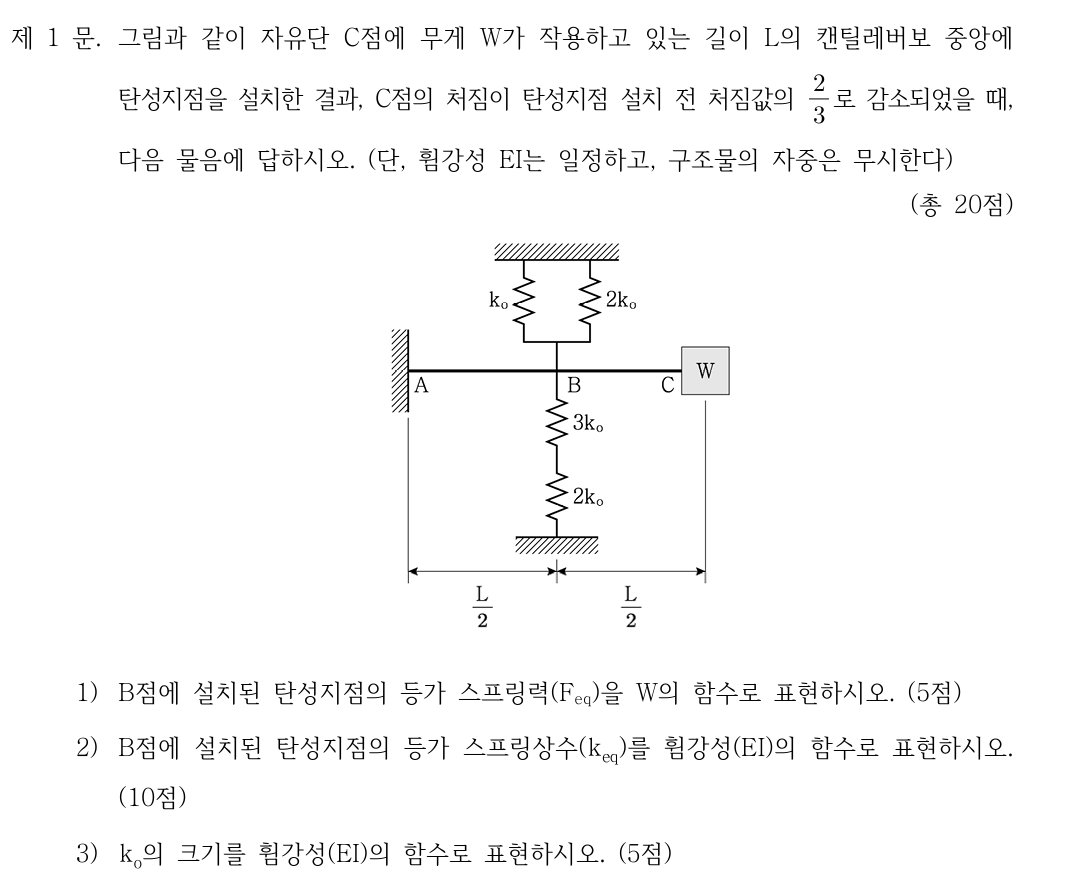
이번 문제는 캔틸레버 ABC 구조에서 C점의 처짐이 기존의 3분의 2로 줄어들도록 하는 외력,
즉 등가 스프링력을 먼저 구하는 것을 목표로 합니다.
첫 번째 단계에서는, 캔틸레버의 끝단 C점 처짐을 기준으로 설정한 뒤, 이 처짐을 줄이기 위해 B점에 설치된 탄성지점이 보에 가하는 힘을 계산합니다. 이 힘이 바로 등가 스프링력이 됩니다.
두 번째 단계에서는, 위에서 구한 값을 이용하여 B점의 실제 처짐을 계산하고, 이를 통해 등가 스프링 상수를 구하게 됩니다.
즉, 보의 강성과 길이에 따라 스프링이 얼마나 저항하는지를 나타내는 값입니다.
마지막으로, 문제에 제시된 스프링의 연결 형태(병렬 및 직렬 연결) 를 이용해기준 스프링 상수인 k₀에 대한 관계식을 세우고,
앞서 구한 등가 스프링 상수와 같다고 두어 최종적으로 식을 완성합니다.
결과적으로, 본 문제는
- C점 처짐 감소 조건으로 등가 스프링력을 구하고,
- B점 처짐으로부터 등가 스프링 상수를 도출한 뒤,
- 스프링 연결 관계로부터 k₀를 계산하는 단계적 해석 과정으로 구성되어 있습니다.
2. 문제 풀이
1) 번 문제

이 문제를 풀기 위해 모멘트 면적법을 통해 C 점에 하중 재하시 중점인 B점의 처짐을 산정할 것 입니다.
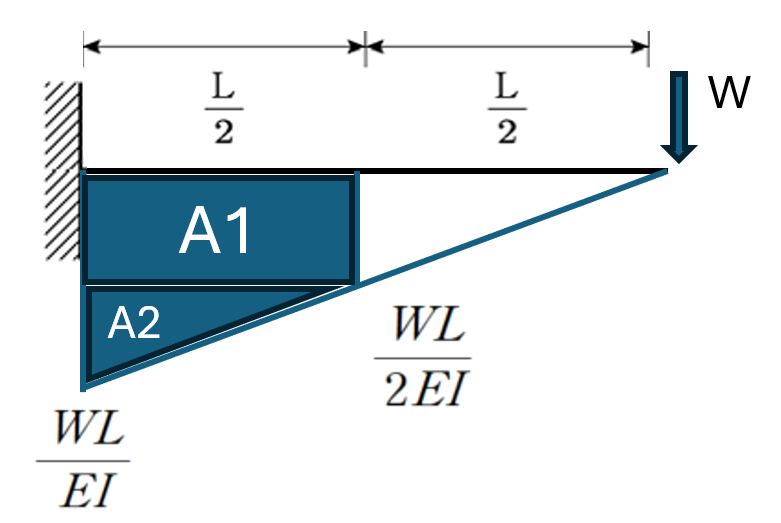


이 식을 통해 C점에 단위 하중이 재하시 B점의 처짐, 즉 유연도 (Flexibility)를 산정 할 수 있습니다.

이때 맥스웰-베티 법칙에 의하여 C점에 단위 하중이 재하시 B점의 처짐(fBC)은 B점에 단위 하중이 재하시 C점의 처짐(fCB)와 동일합니다.
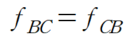
따라서 C점의 처짐을 2/3 배 만드는 하중 F는 다음과 같이 산정 할 수 있습니다.
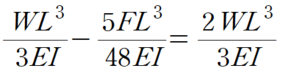
따라서 위의 방정식을 풀면 F의 값은 다음과 같습니다.
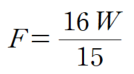
2) 번 문제
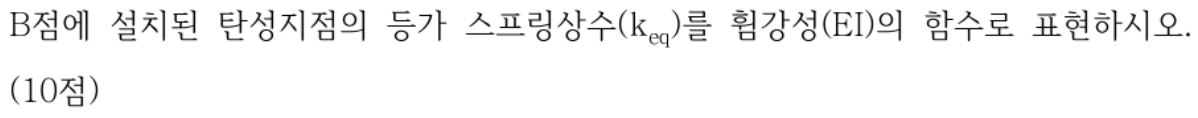
등가 스프링력에 따른 B점의 처짐을 산정하고 해당 처짐이 등가 스프링력의 몇 배인지 구하면 됩니다. (keq × δB=F)
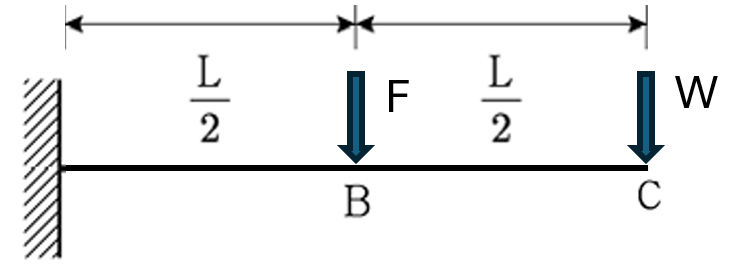

따라서 등가 스프링 상수는 다음과 같습니다.
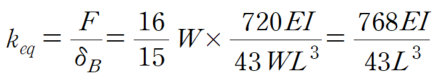
3) 번 문제

스프링의 병렬, 직렬 연결을 활용하여 등가 스프링상수와 동일한 ko를 산정하면 됩니다.
(1) 상부의 스프링 연결
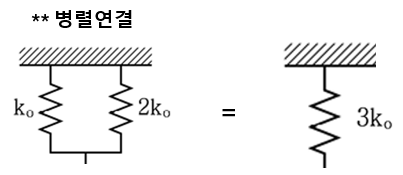
(2) 하부의 스프링 연결
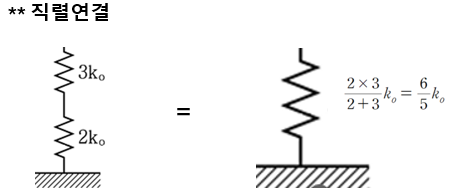
(3) 상하부 스프링의 병렬 연결 = 등가 스프링 상수
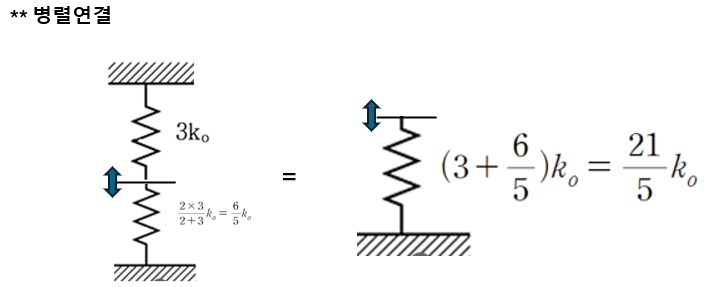
등가스프링상수를 만족하는 k₀ 산정
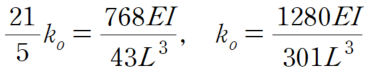
3. 검산 방법 (매트릭스 방법)
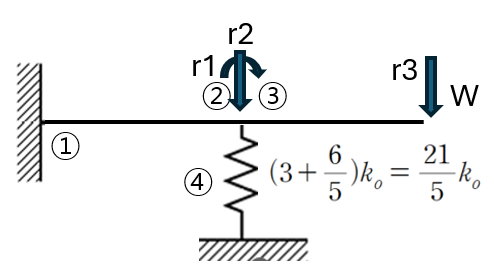
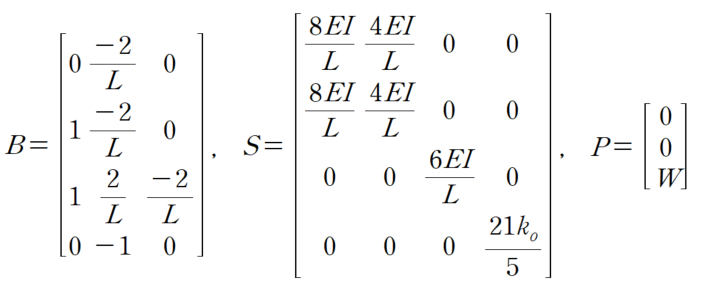
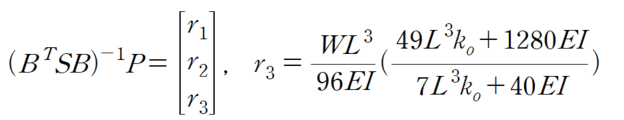

4. 마무리 하며
이번 문제는 스프링의 직렬·병렬 개념을 활용하여 깔끔하게 해결할 수 있는 문제입니다.
처음에는 출제자가 어떤 흐름으로 문제를 유도하려는지 잠시 혼란스러웠지만,
등가 힘과 등가 스프링 상수를 먼저 산정하는 흐름을 하나씩 따라가다 보니
전체 해석 과정이 자연스럽게 맞춰졌습니다.
특히 변위법에 익숙한 수험생이라면
문제의 전개가 논리적으로 이어져 있어 검증이 빠르게 이루어질 것입니다.
반대로 변위법을 처음 배우거나 익히고 있는 수험생에게는
이 문제를 통해 구조해석의 흐름과 사고 과정을 체계적으로 익힐 수 있는 좋은 기회가 될 것입니다.