2025년 7급 응용역학 가형 22번 풀이 (공액보법으로 푸는 방법)

1. 개요

블로그를 처음 운영하던 시기에, 이 문제를 보기를 활용하여 계산 없이도 정답을 추론하는 방법에 대해 소개한 적이 있습니다.

그동안 여러 해의 7급·9급 응용역학 기출문항을 분석하면서 느낀 점은,
보기를 잘 활용하면 정답 범위를 상당히 좁힐 수 있는 문제들이 꽤 많다는 것입니다.
특히 강성도(Stiffness), 유연도(Flexibility), 처짐(Deflection) 등에 대한 감각이 쌓여 있을수록 그러한 문항을 빠르게 식별하고 접근할 확률이 높아집니다.

다만, 비전공자이거나 아직 감각이 형성되지 않은 수험 초기 단계에서는 무리하게 보기를 중심으로 풀이하려는 접근이
오히려 정답률을 낮출 수 있다는 점도 함께 말씀드리고 싶습니다.

 

이러한 이유로 이번 글에서는 공액보법(Conjugate Beam Method) 을 활용하여
처짐 문제를 보다 직관적이고 간단하게 해결하는 방법을 함께 소개해 드렸습니다.
해당 문제를 풀기 위한 일반식과 정석적인 이중적분(Deflection Integration) 방법은
이전 글에 자세히 정리해 두었으니 함께 참고해 주시기 바랍니다.

https://oreostructure.tistory.com/2

2025년 7급 응용역학 가형 22번 풀이

 

2. 풀이 방법

참고로 이번 글에서 소개한 공액보법의 스마트한 적용 방식은 보부재의 유연도를 혼합활용하는 방법으로서
시중 교재에도 없을 뿐만 아니라 온라인에서 본 블로그가 최초로 제시한 풀이 방식이라 자부합니다.

(1) 반력 산정 및 BMD 작도

• 반력은 집중하중 기준 양끝단으로 부터 거리가 3:1 이므로 반력은 1:3으로 나눠 갖게 됩니다.
  따라서 VA=6kN, VB=18kN 입니다.
• 집중하중이 가해지는 지점의 모멘트는 6×9=54 kNm 입니다.

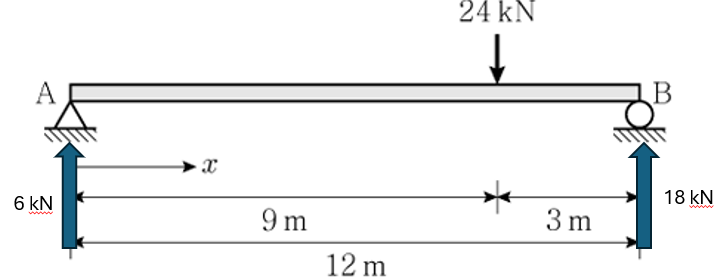
(2) 공액보 적용

• BMD를 통해 M/EI 에 따른 분포하중이 가해지는 단순보인 공액보로 치환할 수 있습니다.
• 이때 공액보의 A지점에 작용하는 수직 반력은 다음과 같습니다.

• 따라서 임의의 x 지점에서의 처짐은 공액보상에서 임의의 x 지점의 모멘트에 해당합니다.

(2) 최대 처짐 산정

• 처짐값을 미분하여 ０으로 만들거나 위의 공액보에서 전단력이 ０이 되는 지점을 찾으면 최대 처짐의 발생하는 위치가 산정됩니다 .

반응형

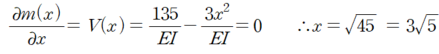
３. 마무리하며

공액보법을 사용할 때 가장 실수가 많이 발생하는 부분은,
공액보로 모델링한 후 평형방정식을 이용해 반력을 직접 계산하는 과정입니다.
이 과정에서 시간은 많이 소요되고,
조금만 계산이 어긋나도 엉뚱한 값이 나오기 쉽습니다.

 

따라서 가능하다면 제가 포스팅에서 소개한, 그리고 인터넷상에서 최초로 공개하는

‘오레오구조식 공액보법’ 을 활용하시기 바랍니다.
이 방식을 사용하면 공액보의 반력을 훨씬 빠르고 간단하게 산정할 수 있으며, 계산 실수 또한 최소화할 수 있습니다.

또한, 이번 문제는 실력자 입장에서는 계산 과정 없이도 10초 내에 끝낼 수 있는 유형입니다.

따라서 이전 포스팅을 함께 참고하시어,
처짐·강성도·유연도에 대한 사고 방식을 어떻게 정리해야 하는지,
그리고 보기를 효율적으로 활용하는 방법이 무엇인지 꼭 확인해 보시기 바랍니다.