보 구조물 변위법의 기본 - 처짐각법 pt 3 (FEM 과 등가 절점 하중)
1. 개요
(1) 등가 절점하중(Equivalent Nodal Force)의 개념
구조역학을 공부하다 보면 “등가 절점하중(또는 등가 격점하중)”이라는 개념이 자주 등장합니다.
이 용어는 단순히 수식의 변환이 아니라, 전산 구조해석의 핵심 개념 중 하나입니다.
이번 글에서는
“단순보 정중앙에 집중하중이 작용할 때, 양 끝단의 회전량을 구하시오.”
라는 간단한 예제를 통해 등가 절점하중이 왜 필요한지, 그리고 어떻게 쓰이는지 살펴보겠습니다.
(2) 전산 구조해석의 기본 관점 — Node 중심 사고
현대의 구조해석 프로그램(FEM, Frame Analysis 등)은 대부분 ‘절점(Node)’ 중심으로 사고합니다.
즉, 부재(Element) 내부에서 어떤 변형이 일어나더라도,
그 결과를 절점에서의 힘과 변위로 환산하여 해석합니다.
이 방식은 여러 가지 장점을 갖습니다.
- 전산 자동화가 용이합니다.
→ 구조물 전체를 매트릭스로 표현할 수 있고, 컴퓨터 연산에 적합합니다. - 선형 해석 이론과 궁합이 좋습니다.
→ 미소변형을 가정하면 하중과 변위의 관계가 선형이 되어, 매트릭스 계산으로 결과를 도출할 수 있습니다.
따라서 전산 구조해석의 기반을 이해하기 위해서는
변위법(Displacement Method), Local·Global 좌표계, 그리고 유한요소법(FEM)에 대한 개념을 익히는 것이 필수적입니다.
(3) Element 내부의 하중은 어떻게 처리될까?
그렇다면, 부재(Element) 내부에 작용하는 하중이나
온도 변화, 제작 오차 등의 ‘부재 내부에서 발생하는 효과’는 어떻게 처리할까요?
이런 하중들은 직접 Node에 작용하지 않기 때문에,
컴퓨터가 인식할 수 있도록 절점하중 형태로 변환해야 합니다.
바로 이 과정을 등가 절점하중(Equivalent Nodal Force)으로의 변환이라고 합니다.
즉,
“부재 내부에 작용하는 실제 하중의 효과를,
동일한 영향(변위·모멘트·전단력 등)을 주는 절점하중으로 바꿔주는 것”
이 바로 등가 절점하중의 개념입니다.
2. 예제를 통해 보는 등가 절점 하중
(1) 간단한 예제로 보는 개념 이해
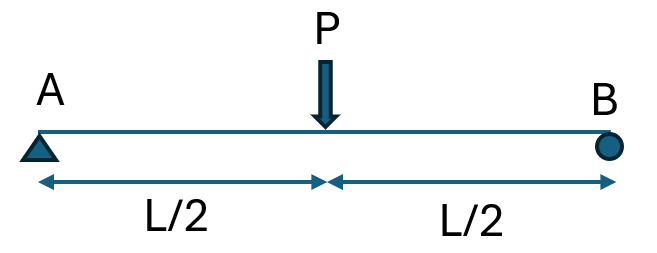
예를 들어, 단순보 중앙에 집중하중 P가 작용한다고 가정해봅시다.
이 하중이 있을 때 실제로는 보의 중앙에서 처짐이 발생하고,
양 끝단에서는 회전이 발생합니다.
하지만 전산 프로그램은 “중앙”이라는 점을 별도의 Node로 정의하지 않는 한,
그 하중을 직접 다룰 수 없습니다.
그래서 우리는 이 중앙 집중하중 P가 양 끝단의 절점(Node)에 어떤 영향을 주는가를 계산해,
이를 “등가 절점하중”으로 치환합니다.
그 결과 양 끝단의 회전량(또는 반력, 모멘트)을 등가 절점하중의 형태로 표현할 수 있게 됩니다.
(2) 중앙 집중하중에 대한 FEM

FEM의 유도 과정은 다음 포스팅에서 다룰 예정입니다.
이번에는 부재 내에 하중이 작용할 때, 양단이 고정되어 있다면 어떤 모멘트가 생기는가,
즉, 고정단 모멘트(FEM)가 존재한다는 사실 자체를 인지하고 이해하는 것이 핵심입니다.
① 고정단에서 왜 모멘트가 생기는가?
단순보(양단 힌지)였다면, 하중을 받으면 양 끝단이 자유롭게 회전각(θ) 을 가질 수 있습니다.
그러나 고정보는 단부의 회전이 완전히 구속되어 회전각이 0이 되어야 합니다.
즉, 하중에 의해 생기려는 회전을 억제하기 위해
단부에서는 그 회전을 막는 모멘트(=고정단 모멘트, FEM)가 발생합니다.
이 FEM은
“하중에 의해 발생하려는 처짐이나 회전을 보정하기 위해 단부가 스스로 만들어내는 반작용 모멘트”
라고 볼 수 있습니다.
② FEM의 물리적 의미
- 하중이 작용하면 보가 아래로 휘려 합니다.
- 그런데 단부가 회전할 수 없으므로, 단부는 이를 막기 위해 반대 방향으로 휨 모멘트를 생성합니다.
- 이때 단부에 생긴 이 반대 방향 모멘트가 바로 Fixed End Moment (FEM) 입니다.
즉, FEM은 구조물이 하중을 받았을 때
“고정 조건을 유지하기 위해 필연적으로 생기는 단부의 내력”을 의미합니다.
(3) 처짐각법 적용 통한 양 끝단 회전량 산정

이때 집중 하중 P의 효과를 양쪽 끝단에 분배하여 다음과 같이 표현 할 수 있습니다.
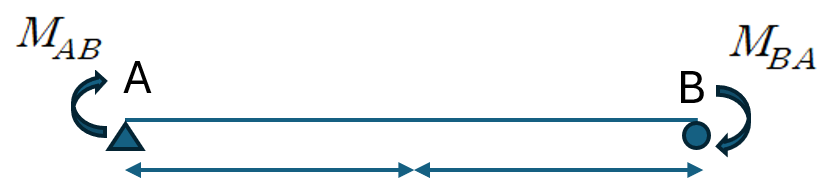

본래 단순보였기 때문에 양끝단의 모멘트는 0입니다. 따라서 다음과 같이 서술할 수 있습니다.

FEM 부분을 우측변으로 넘기면 다음과 같이 표현됩니다.

따라서 FEM값을 대입하여 값을 구하게 되면 다음과 같습니다.

연립해서 풀게 되면 회전각음 다음과 같이 산정됩니다.

3. 마무리하며
먼저 FEM(Fixed End Moment)이란,
하중이 작용했을 때 단부 회전을 막기 위해 구조 내부에서 스스로 생기는 모멘트입니다.
즉, FEM은 외부에서 가해진 힘이 아니라,
부재가 고정 조건(회전각 θ=0) 을 유지하기 위해
내부적으로 반작용하는 내력(Internal resisting moment) 입니다.
등가 절점하중은 FEM이나 분포하중을 절점에 작용하는 외력 형태로 표현한 것입니다.
즉, 내부에서 생긴 FEM을 외력으로 다시 표현해야
절점 평형식(∑M=0, ∑F=0)을 세울 수 있습니다.
그런데 내부 반력(FEM)을 외력으로 표현하려면,
방향을 반대로 뒤집어야 합니다.
왜냐하면,
내부 반력(FEM)은 구조 내부가 받는 힘이고,
등가절점하중은 구조 외부가 받는 힘이기 때문입니다.
이것이 바로 등가절점하중이 FEM의 “마이너스”로 나타나는 이유입니다.