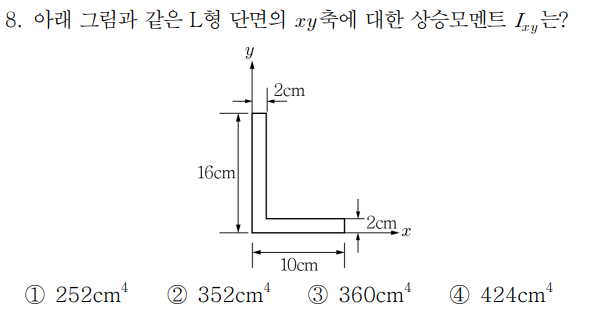
2015년 7급 서울시 응용역학 8번 (Ixy 단면상승모멘트)
1. 개요
문제는 Ixy 단면상승모멘트에 대해 물어보는 유형이며 이에 더해 중립축 정리까지 하는 유형입니다.
단면이 대칭축이 몇개 있느냐에 따라 단면상승모멘트는 달라지는데, 이에 대해 알아보고 문제를 풀어보는 방법으로 포스팅을 진행하겠습니다.
2. 개념 설명
(1) 상승 모멘트 (Ixy)
상승 모멘트 Ixy는 다음과 같이 정의할 수 있습니다.

이 값은 단면이 기울어진 경우 또는 대칭이 아닌 경우 반드시 존재하게 됩니다.
(2) 2축 대칭 단면
대표적으로 폭이 b 이고 높이가 h 인 직사각형 단면을 생각해볼 수 있습니다. 단면의 도심을 기준으로 상승모멘트 (Ixy)를 산정하면 다음과 같습니다.


2축 대칭 단면에 대해서 Ixy (상승모멘트)의 값은 0 입니다.
하지만 이 단면이 기울어지게 되면 이야기가 달라집니다.
좌표축 회전에 따른 Ixy는 다음과 같이 산정할 수 있습니다.

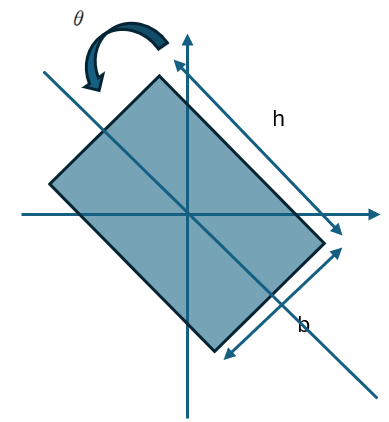
따라서 반시계 방향으로 θ 만큼 기울어진 직사각형 단면의 상승 모멘트는 다음과 같이 표현 할 수 있습니다.
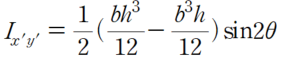
(3) 정다각형
대표적으로 한변의 길이가 b인 정사각형 단면을 생각해볼 수 있습니다. 기본적으로 적어도 하나의 축에 대해 대칭이므로 상승모멘트는 0으로 표기할 수 있습니다.
회전하게 되면 어떻게 될까요?
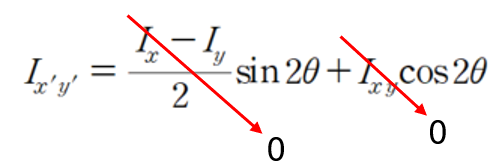
회전을 해도 항상 상승모멘트는 동일하게 0이 됩니다.
정다각형 단면에 대해서는 상승모멘트가 0 이며 단면이 회전되어도 항상 0이 된다.
(4) 단면 상승 모멘트의 평행축 정리
결론적으로, 상승 모멘트( Ixy)는 구조가 평행축 정리와 유사한 형태를 가지지만,
거리의 제곱( d^2 )이 단면적에 곱해지는 것이 아니라, x축 방향 거리와 y축 방향 거리의 곱이 면적요소에 곱해진 꼴이 됩니다.

3. 문제풀이

(1) 단면의 구분
단면을 편의상 2부분으로 구분하여 윗사각형을 A1, 아랫사각형을 A2로 지칭하겠습니다.
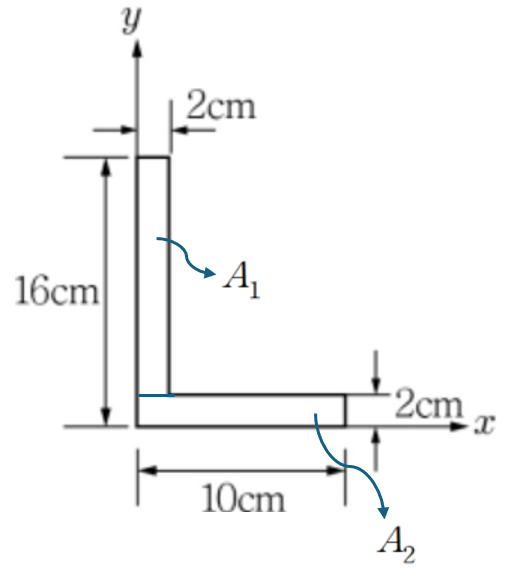
(2) 평행축 정리 활용

A1, A2 모두 Ixy= 0 이므로 Δx × Δy×A 만 고려하면 된다.

답은 ②번이다.
4. 마무리하며
단면의 성질은 다양한 시험에서 지속적으로 반복 출제되는 핵심 영역입니다.
특히 단면상승모멘트(Products of Inertia 변화) 를 논할 때에는
단면에 대칭축이 1개인지, 2개인지에 따라 성질이 완전히 달라지므로
그 차이를 반드시 정확히 알고 계셔야 합니다.
일반적으로
- 대칭축이 2개인 단면(직사각형, 원형, H형강 등)은
제품모멘트 이 항상 성립합니다. - 대칭축이 1개만 있는 단면(비대칭 T형, 반원, 일부 복합 단면 등)은
회전 축에 따라 Ixy≠0 이 되며, 좌표축을 회전시키면 값이 변화합니다.
단면상승모멘트를 직접 계산하는 문제는 자주 출제되지는 않지만,
그 계산 과정은 사실 응력·변형률 모어원(Mohr’s Circle) 과 구조가 완전히 동일합니다.
즉, 응력 변환 공식에서 τ자리에 −Ixy 를 그대로 대입한다고 생각하면 됩니다.
따라서 혹시 신유형으로 “회전된 축에 대한 를 구하라”
라는 문제가 나오더라도, 이는 응력 변환 공식을 그대로 적용하는 것과 다르지 않다는 점을 기억하시면
충분히 대처가 가능합니다.
결국 핵심은, 단면 2차모멘트의 평행축 정리 + 모어원 구조 + 대칭성 판단
이 세 가지를 정확히 이해하고 있으면
단면 성질 문제는 어떤 형태로 출제되더라도
안정적으로 대응할 수 있다는 것입니다.