2009년 7급 국가직 응용역학 4번 문제 (등가절점하중 + 변위일치 해법)

1. 개요
위 문제는 3차 부정정 Frame 구조물의 해석을 요구하는 동시에,
구조적으로 상당히 흥미로운 특징을 갖고 있습니다.
우선 구조 자체는 BC와 AD의 중점을 연결하는 선을 기준으로 완전한 기하학적 대칭을 이루고 있습니다.
그러나 하중은 이 대칭축을 기준으로 크기는 동일하나 방향이 반대인 역대칭 하중이 작용하고 있습니다.
그렇다면 구조는 대칭이고 하중이 역대칭일 때,
구조물 내부에서 발생하는 내력(모멘트·전단력·축력)은 어떻게 분포될까요?
결론부터 말씀드리면,
내력 또한 역대칭 형태로 전개됩니다.
이를 부재 BC를 예시로 살펴보겠습니다.
- 만약 하중까지 대칭이라면, BC 부재는 순수 굽힘(Pure Moment) 상태가 되며 전단력은 존재하지 않습니다.
- 그러나 이번 문제처럼 하중이 역대칭이면,
B 지점에서의 모멘트가 –M이었다면 대칭축을 지나 C 지점에서는 +M으로 바뀌며,
중점에서는 반드시 모멘트가 0이 됩니다.
이와 같은 내력 분포는 대칭 구조 + 역대칭 하중이라는 조건 아래에서
전형적으로 나타나는 내력 전개 방식이며,
구조물 전체의 해석을 크게 단순화시키는 중요한 성질입니다.
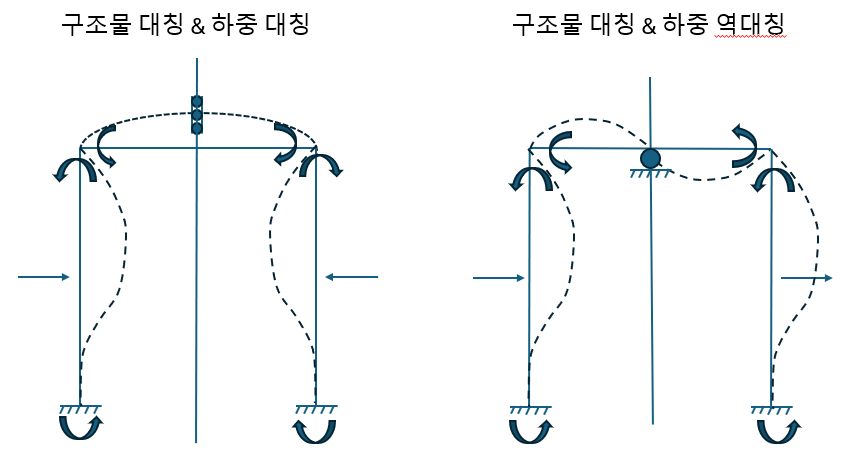
따라서 구조물 대칭 & 하중 대칭에서는 Fixed roller로 모델링이 가능하며
구조물 대칭 & 하중 역대칭인 경우 Roller로 모델링이 가능합니다.
2. 문제풀이
위에 서술한대로 구조물 대칭 & 하중 역대칭 관계속에서는 대칭축을 기준으로 Roller로 모델링이 가능합니다.
이로서 기존의 3차 부정정 구조물이 1차 부정정 구조물로 단순화 되었습니다.
시험장에서 등가절점하중을 활용하여 쉽게 풀이 할 수 있는 방식을 소개할 까 합니다.

2-1. 등가절점하중을 활용한 풀이 방법
부재 중간에 작용하는 P를 절점에 작용하는 등가절점하중 (Equivalent Nodal Force)으로 치환하여 해석해보겠습니다.
절점 B는 Rigid Joint (강절점) 이므로 내력 (모멘트)가 존재합니다. 이 내력은 θBA와 θBC을 동일하게 만들어주는 역할을 합니다.
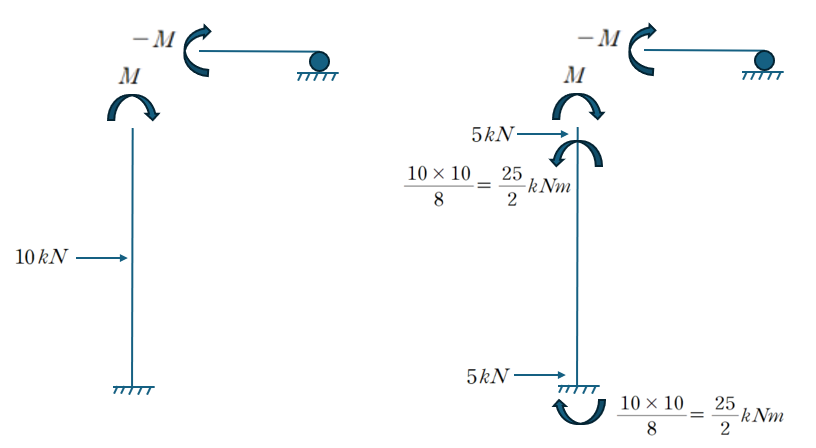
하중 10kN를 우측 그림과 같이 절점에 작용하는 등가 절점하중으로 치환하였습니다.
절점에서 작용하는 하중을 바탕으로 θBA와 θBC가 동일하다는 적합방정식을 세워보겠습니다.
캔틸레버에 수직하중과 모멘트가 작용했을때의 회전각 공식을 활용하여 θBA를 산정하면 다음과 같습니다.

처짐각법 공식을 활용하여 θBC를 산정하면 다음과 같습니다.

θBA= θBC 라는 적합방정식을 세워 풀어보면 다음과 같습니다.

이를 M에 대해 풀면 다음과 같습니다.
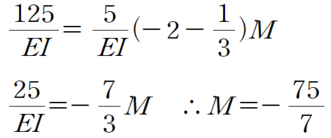
따라서 답은 ③번이 됩니다.
3. 마무리하며
등가 절점 하중 개념을 활용하는 방법과 구조물과 하중의 대칭 역대칭을 활용하여
단순화하고 빠르게 문제를 해결하는 방법을 살펴보았습니다.
절점에서 단순한 변위 적합식만 세워도 문제의 핵심에 바로 다가갈 수 있다는 점에서
등가절점하중은 매우 강력한 도구라고 생각합니다.
앞으로도 기회가 되면 해당 문제를 다른 관점과 다른 해석 기법으로도 풀이할 수 있는 방법들에 대해 소개하겠습니다.
또한 많은 분들이 어려워하는 주제인 Sway (횡변위)가 있을 때 구조물에서의 모멘트 분배법에
대해서도 다음에 다뤄보도록하겠습니다.