2024년 9급 지방직 응용역학개론 (좌굴 mode에 대한 이론)

1. 개요

https://oreostructure.com/64

2024년 9급 지방직 응용역학개론 풀이

과거에 2024년 9급 지방직 응용역학 풀이를 올리면서, 당시 18번 문항에 대해 더 자세한 설명을 추후 다루겠다고 말씀드린 적이 있습니다.
그 문제의 핵심은 사실 좌굴하중과 좌굴모드(Buckling Mode) 에 대한 이해입니다.
해당 문항 자체는 단순히 유효좌굴길이(Effective Length) 를 적용하면 쉽게 풀리는 문제였습니다.
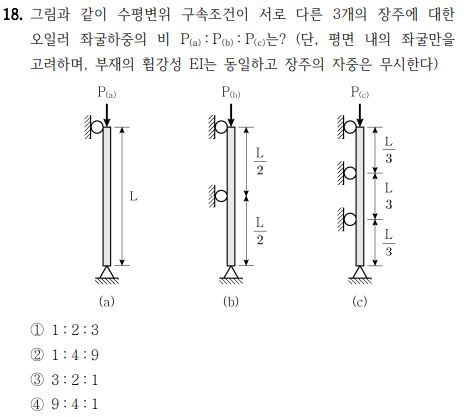
그러나 좌굴 모드에 대한 감각이 있는 분들은, 문제를 보는 순간 아래와 같은 이미지를 즉시 떠올리실 수 있었을 것입니다.

• (a) 형태 → Pin-Pin 조건의 1차 모드(기본 모드)
• (b) 형태 → Pin-Pin 2차 모드
• (c) 형태 → Pin-Pin 3차 모드

즉, 좌굴 모드의 형상만 보아도
“아, 이건 유효길이가 L, ½L, ⅓L 로 바뀌는 전형적인 Pin-Pin 모드구나”
라는 판단이 금방 서게 됩니다.
이번 글에서는 이전 풀이에서 다 하지 못했던 이 좌굴모드 개념을 좀 더 직관적으로 설명드리고자 합니다.
좌굴은 단순히 공식을 대입하는 문제를 넘어서, 지점 조건과 모드 형상을 함께 이해해야 하는 분야입니다.
따라서 이러한 기본 모드 형상에 익숙해지면, 실제 시험에서도 훨씬 빠르고 정확하게 해결할 수 있습니다.

2. Pin-Pin 조건의 좌굴 해석

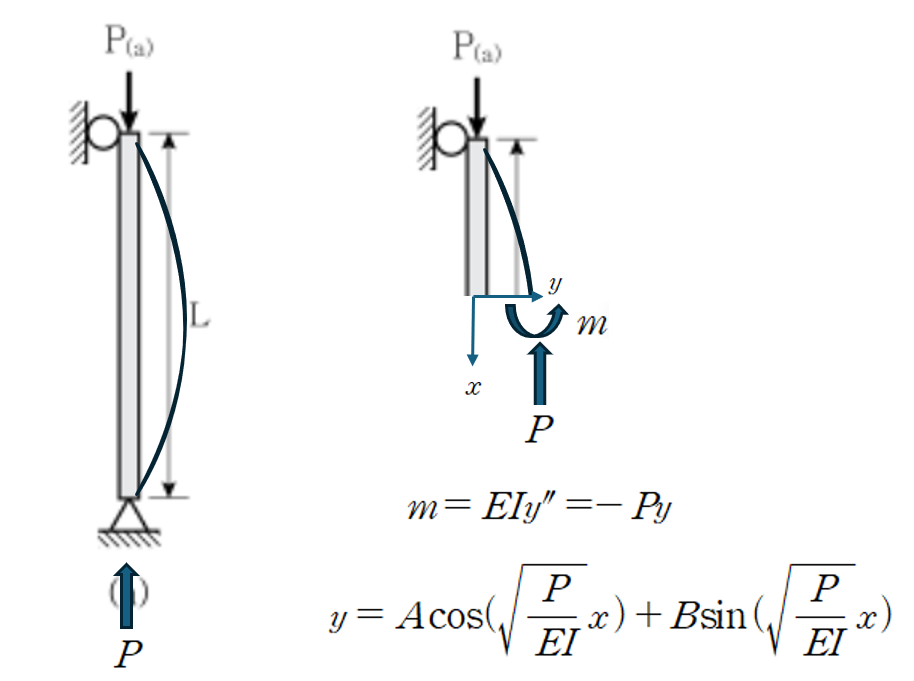
경계조건 (Boundary Condition) 적용시 다음과 같습니다.

A와 B는 0이 아니므로 Trivial Solution을 피하기 위해 행렬값의 determinant가 0이 되어야 합니다.

따라서 다음과 같은 결론을 내릴 수 있습니다.

즉, sin 값이 0이 되게 하는 값은 N이 자연수인 무수히 많은 값들이 존재하며
 

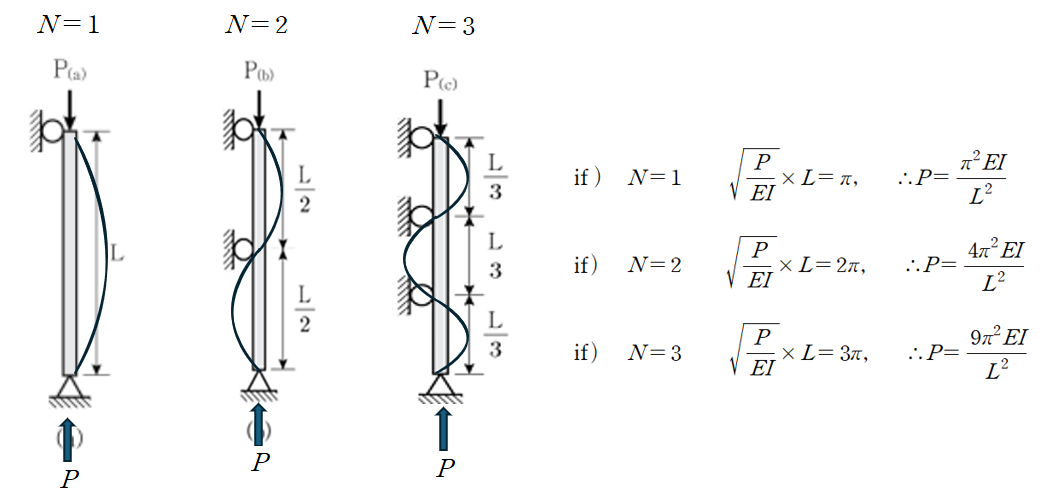
따라서 위 문제의 답은 쉽게 ②라는 것을 재 검증할 수 있습니다.

2. Roller로 지지된 (b)의 구조해석 (심화 주제)

압축을 받고 있는 2개의 기둥에 대해 다음과 같이 자유물체도 (Free Body Diagram)을 그릴 수 있습니다.

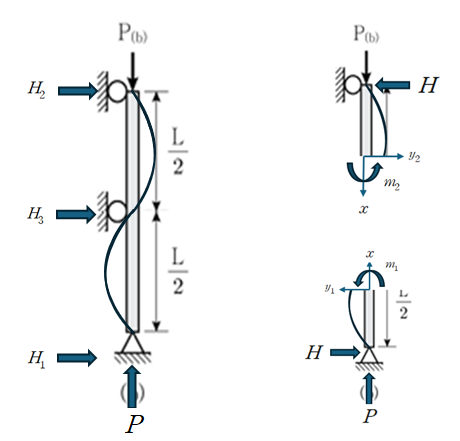
아랫 기둥에 대해 다음과 같이 미분 방정식을 세울 수 있습니다.

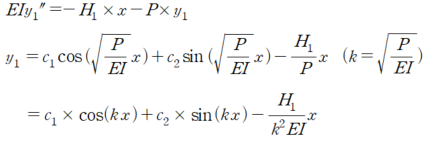
윗 기둥에 대해 다음과 같이 미분 방정식을 세울 수 있습니다.

그리고 이에 대한 경계 조건은 다음과 같습니다.

이를 행렬로 표현해보겠습니다.

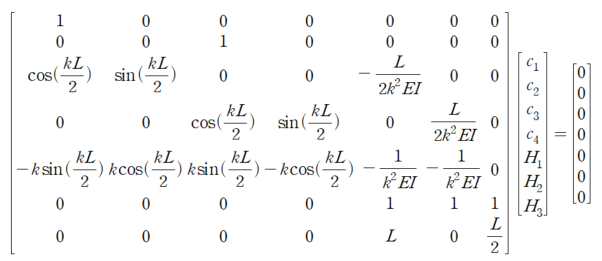
Non-Trivial solution을 위해 좌측 행렬값의 Determinant를 구해보면 다음과 같습니다.

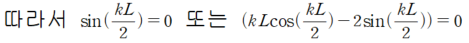
이중 작은 값을 산정하는 것이므로 포스팅 초기에 올렸던 N=2에 대한 좌굴 하중값을 확인 할 수 있습니다.
두개의 값에 대한 좌굴 형상은 대략 어떻게 될까요?
좌굴 발생시 정확한 처짐형상은 알 수 없지만 대략적인 Mode 파악은 가능합니다.

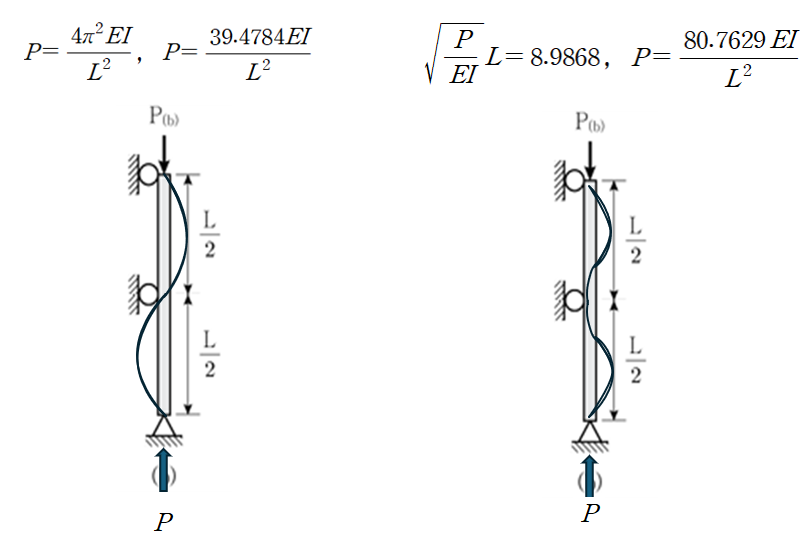
(b)구조물에서 2번째 mode 좌굴 발생시에는 중간 Roller지점의 기울기가 0인 것을 확인 할 수 있습니다. 
이는 대칭구조물에서 하중도 대칭 발생시 Fixed-Roller로 모델링 하는 것과 동일합니다.
Roller로 수평이동도 추가 고정되어있으니 이는 고정단과 일치하게 됩니다.
따라서 (b)기둥의 2번째 mode 좌굴하중값은 다음 구조물의 좌굴하중과 일치하게 됩니다.

2. Roller로 지지된 (c)의 구조해석 (심화 주제)

미분방정식의 덩어리가 너무 커지고 변수가 많아져서 불가피하게 대칭 모델링을 활용하겠습니다.

윗기둥의 미분방정식은 다음과 같이 세울 수 있습니다

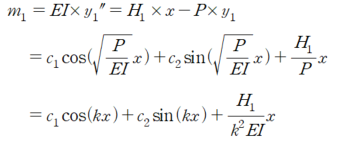
아랫 기둥의 미분방정식은 다음과 같이 세울 수 있습니다.

적용하는 경계조건 (Boundary Condition)은 다음과 같습니다.

이를 행렬로 표현해 보겠습니다.

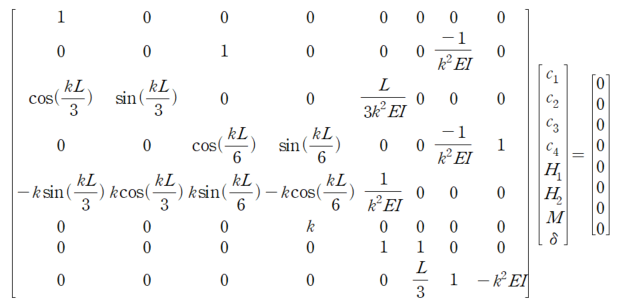
마찬가지로 행렬식의 Determinant를 구해보면 다음과 같습니다.

붉은색 Box의 값이 0이 되는 값은 kL=3π 일 때 입니다. Pin-Pin 좌굴에서 3번째 모드와 동일합니다.

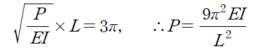
4. 마무리 하며

제가 이전 글에서 “좌굴하중을 보면 대략적인 좌굴 형상을 미리 알 수 있다”고 말씀드린 이유는,
좌굴하중이 고유값(eigenvalue) 에 해당하고,
좌굴모드 형상이 고유벡터(eigenvector) 에 해당하기 때문입니다.
즉, 구조물이 좌굴하려는 순간의 모드는 단순히 ‘그럴 것 같다’라는 감이 아니라,
엄밀히 말해서 특정 고유값 문제를 풀었을 때 나타나는 해의 형태입니다.
그래서 보나 기둥의 지점 조건만 알면, 그 구조물이 어떤 모드로 좌굴할지를 비교적 쉽게 예상할 수 있는 것입니다.
이번 포스팅에서 다룬 심화 주제들은 연산이 다소 복잡해 보일 수 있습니다.
하지만 사실은 모두 같은 풀이 흐름(Flow) 을 따르고 있습니다.

1. 해당 구조의 경계조건(Boundary Conditions)을 정확히 설정하고,
2. 이를 바탕으로 행렬식(Matrix Equation)을 구성한 뒤,
3. 자명하지 않은 해(Non-trivial Solution) 를 얻기 위해
   행렬식의 Determinant = 0 조건을 적용하는 것입니다.

이 방식은 단순기둥 좌굴부터, 프레임 좌굴, 보-기둥 상호작용 좌굴까지
모든 좌굴 문제의 공통된 접근법입니다.
향후 기회가 된다면, 좌굴 이론에 대해 정리하는 포스팅을 올리도록 하겠습니다. 
좌굴 이론은 알고 나면 두 번 다시 어렵지 않지만,
처음에는 접근법 자체에 익숙해지는 과정이 필요합니다.
앞으로도 이 블로그를 통해 그 감각을 자연스럽게 익히실 수 있도록 정리해 드리겠습니다.