
1. 개요
보통 이러한 유형의 문제는 단위하중법(Unit Load Method) 을 이용해 푸는 경우가 많습니다.
하지만 이번에는 단위하중법 대신 ‘자유도(Degree of Freedom)’ 의 개념으로 구조물을 분석해 봅시다.
이 접근법은 계산 과정을 단순화하면서도 문제의 본질을 훨씬 명확하게 파악할 수 있는 강력하고 효율적인 방법입니다.
특히 이러한 시각은 2025년 7급 응용역학 24번 문제와 같은 유사 유형을 빠르고 정확하게 해결하는 데 큰 도움이 됩니다.
해당 구조물은 정정 트러스(Statically Determinate Truss) 입니다.
이유는 구해야 할 부재력이 5개이고, 세울 수 있는 평형방정식 또한 5개이기 때문입니다.
여기에 온도 변화가 발생했다는 조건은 매우 의미 있는 조건입니다.
왜냐하면 온도 변화가 없는 부재는 길이 변형이 일어날 수 없으므로, 강체(Rigid Body)로 취급할 수 있기 때문입니다.
그렇다면 왜 이런 해석이 가능할까요?
그 이유는 정정 구조물에서는 온도 변화, 제작 오차, 지점 침하 등이 발생하더라도 새로운 부재력이 생기지 않기 때문입니다.
즉, 이러한 외적 요인들이 구조물 전체의 자유도에 직접적인 영향을 주지 않는다는 뜻입니다.
따라서 온도 변화가 생긴 각 부재가 전 구조물의 자유도(Global DOF) 에 어떤 영향을 미치는지를 파악하면,
문제를 훨씬 직관적으로 해결할 수 있습니다.
이 전략은 온도 변화뿐만 아니라 제작 오차, 지점 침하와 같은 다른 특수 조건 문제에도 그대로 적용할 수 있습니다.
핵심은 각 부재의 변형(Local DOF, 부재 자유도) 이 전체 구조물의 거동(Global DOF)에 어떤 형태로 연결되는지를 파악하는 것입니다.
2. Global DOF , Local DOF

Global DOF, 즉 전 구조물의 자유도는 각 절점(Node)마다 x방향과 y방향 한 개씩 존재합니다.
이는 구조물에 변형이 생기더라도, 2차원(2D) 구조물의 특성상 두 축 방향에서만 움직일 수 있기 때문입니다.
설명의 편의를 위해,
전 구조물의 자유도는 r₁ ~ r₅로,
각 부재의 자유도(Local DOF)는 ① ~ ⑤로 표기하겠습니다.
한편, Local DOF가 부재마다 1개씩만 존재하는 이유는
트러스 부재가 오직 하나의 축 방향 변형(즉, 인장 또는 압축)만 허용하기 때문입니다.
트러스 부재는 휨이나 전단에 저항하지 않고, 단지 축 방향으로만 변형할 수 있습니다.
따라서 온도 변화를 받지 않은 부재는 길이 변화가 발생할 수 없으므로 강체(Rigid Body) 로 취급합니다.
즉, ①, ④, ⑤ 부재는 인장 또는 수축이 발생해서는 안 되며,
결과적으로 이 부재들은 구조물의 전체 변형에 참여하지 않습니다.
3. 부재력=0 조건으로 구속되는 자유도
(1) r1, r5
r1 만 존재 할 경우 ⑤ 번 부재의 부재에 압축 변형이 생깁니다.
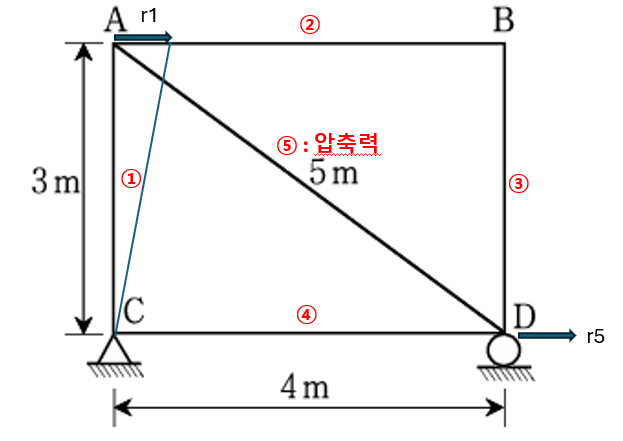
따라서 ①,④,⑤번 부재는 강체로 취급할 수 있다라는 조건에 모순이 생깁니다.
⑤ 번 부재의 길이방향 변화량을 보존하기 위해 r5 만큼 이동한다고 하더라도 ④번 부재가 인장이 생기기 때문에 모순이 생깁니다.

(2) r2
r2가 구속되지 않을 경우 ①과 ⑤에 인장이 생기기 때문에 모순이 발생합니다.

(3) 유효한 자유도
②, ③ 에 온도변화가 생겼다고 하더라도 ①,④,⑤ 는 강체 취급을 하기 때문에 삼각형 ACD는 강체 plate로 취급하면 됩니다.
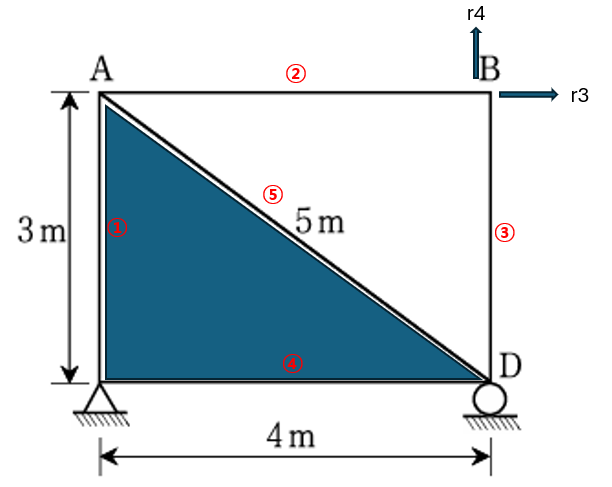
따라서 r3,와 r4만 유효합니다.
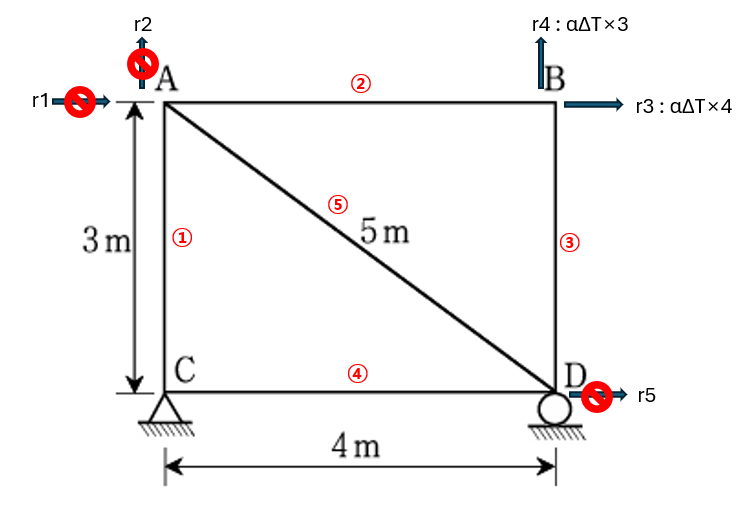
즉, ②,③ 번 부재의 온도 변화는 꼭지점 B의 움직임에만 영향을 주게 됩니다.
4. 문제의 단순화

문제에서 부재의 온도 변화 변화량, 즉, local DOF에 따른 전 구조물의 DOF- Global DOF를 살펴볼때, 지점 D의 움직임에는 온도가 어떠한 영향을 주지 않으므로 과감히 온도에 관련된 문구를 삭제할 수 있습니다. 단순히 D가 수평으로 0.8mm만큼 움직일 때, 하중 P의 최대 값을 구하면 됩니다.
D가 0.8mm 만큼 움직이면 CD 부재가 0.8mm 만큼 움직이게 되므로 CD 부재의 인장력을 산정할 수 있으며 단면법으로 문제를 쉽게 해결 할 수 있습니다.
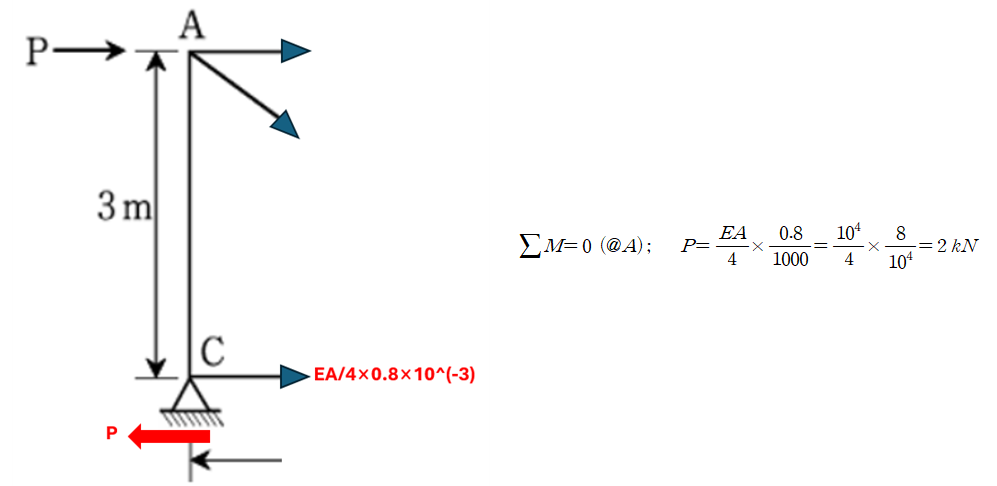
5. 마무리 하며
이해를 돕기 위해 다소 길게 설명하였지만,
실제 시험에서는 정정 트러스 구조물의 Global DOF를 빠르게 파악하는 것만으로도 한 줄의 식으로 문제를 해결할 수 있습니다.
즉, 복잡한 계산이나 단위하중법을 적용하지 않더라도,
각 부재의 변형 가능 여부와 구조물의 전체 자유도를 직관적으로 이해하면
문제를 매우 짧은 시간 안에 풀 수 있습니다.
함께 연구해보면 좋은 예시로는 2025년 7급 국가직 응용역학 24번 문제가 있습니다.
아래 링크를 참고하시면 본 글에서 설명한 원리를 실제 문제에 어떻게 적용할 수 있는지 확인하실 수 있습니다.
'재미있는 문제- 쉬운풀이 > 축 부재 (axial member)' 카테고리의 다른 글
| 2015년 서울시 7급 12번 (축부재의 에너지 산정+심화 개념) (0) | 2025.12.01 |
|---|---|
| 2015년 7급 서울시 응용역학 3번 (온도 상승 + 축부재) (0) | 2025.11.19 |
| 2023년 국가직 7급 9번과 2025년 서울시 7급 14번 비교 (Truss) (0) | 2025.11.08 |
| 2024년 7급 군무원 응용역학 5번 (적분법/ 등가면적법/ 직관적 사고법) (0) | 2025.10.05 |
| 2025년 7급 응용역학 가형 24번 풀이 (0) | 2025.09.27 |