Insight 구조&응용역학

1.개요이번 문제는 최소일의 원리나 카스틸리아노의 정리 등 여러 가지 방법으로 해석할 수 있습니다. 단순히 전달률 (C_AB)와 (C)점의 수직처짐 (δ_CV)만을 구하는 것이 목적이라면 이러한 에너지법을 이용하는 것도 충분히 좋은 접근입니다. 그러나 이번 포스팅에서는 조금 다른 관점에서 문제를 살펴보고자 합니다.이번 풀이의 주된 목적은 처짐각법(Slope-Deflection Method)이 강성 매트릭스 해석법으로 어떻게 자연스럽게 연결되는지를 보여드리는 것​입니다. 처짐각법의 기본식은 부재 단부의 회전각과 절점변위를 이용하여 단부모멘트를 표현합니다. 그런데 여러 부재가 연결된 구조물에서 이러한 관계식을 절점별로 정리하고 평형조건을 적용하면, 우리가 매트릭스 구조해석에서 익숙하게 접하는[K]{d}={P..

1.개요이번 문제는 2경간 연속보에 등분포하중과 집중하중이 작용할 때 지점반력을 산정하는 전형적인 1차 부정정 구조물 문제입니다. 일반적으로 이러한 연속보 문제는 처짐각법이나 3연 모멘트 방정식을 이용하여 해석할 수 있으며, 특정 지점을 부정정력으로 선정한 뒤 변위일치조건을 적용하는 방법으로도 접근할 수 있습니다. 이번 풀이에서는 복잡한 처짐곡선식을 직접 구하거나 적분을 수행하지 않고, 각 경간의 하중을 등가 절점모멘트로 치환한 뒤 B점에서의 회전각 적합조건을 이용하는 방법으로 풀어보겠습니다.특히 등분포하중과 중앙 집중하중에 의한 모멘트도를 이용하면 각 하중을 간단한 등가 절점모멘트로 바꿀 수 있고, 이후에는 B점을 기준으로 양쪽 경간의 회전각이 동일하다는 조건만 적용하면 내부 부모멘트를 매우 빠르게 구..

1.개요해당 문제는 과거 블로그에서도 한 차례 다룬 적이 있습니다.https://oreostructure.tistory.com/17당시에는 지점침하에 의해 발생하는 양단 고정모멘트를 구한 뒤 M/EI도를 그리고, 모멘트-면적법을 이용하여 C점의 처짐을 직접 산정하는 방식으로 풀이하였습니다. 이 방법 역시 계산량이 많지 않고 충분히 좋은 풀이입니다. 이번에는 같은 문제를 조금 다른 관점에서 다시 풀어보려고 합니다.처짐을 묻는 문제라고 해서 항상 EIv′′=M(x)에서 출발하여 처짐곡선식을 만들 필요는 없습니다. 물론 모멘트식을 세우고 두 번 적분한 뒤 경계조건을 적용하면 정석적으로 답을 구할 수 있습니다. 그러나 객관식 시험에서는 동일한 결과를 훨씬 짧은 과정으로 얻을 수 있다면 굳이 긴 계산을 선택할 이..

1.개요구조역학을 공부하다 보면 처짐각법(Slope Deflection Method)은 계산이 많고 풀이 시간이 오래 걸리는 해석법이라는 인식을 갖는 수험생들이 많습니다. 실제로 시중의 교재를 보면 모든 절점의 회전각과 횡변위를 기계적으로 미지수로 설정한 뒤, 부재별 처짐각식을 모두 전개하여 긴 연립방정식을 푸는 방식이 대부분입니다. 이러한 풀이를 처음 접한 수험생 입장에서는 "시험장에서 이런 방법을 어떻게 사용하라는 것인가?"라는 생각이 드는 것도 무리가 아닙니다. 결국 처짐각법은 실전에서는 사용할 수 없는 비효율적인 해석법이라는 오해가 생기고, 많은 수험생들이 모멘트분배법이나 강성법만 익힌 채 처짐각법은 형식적으로만 공부하고 넘어가는 경우가 많습니다.하지만 이는 처짐각법 자체의 한계라기보다 효율적으로..

1.개요캔틸레버 변단면 문제에 이어, 이번에는 한 단계 더 나아간 형태의 변단면 문제를 출제해보았습니다.풀이를 확인하기에 앞서, 반드시 스스로의 방법으로 한 번 고민해보시기를 권장드립니다. 자신의 해법을 점검하고, 이후 타인의 풀이를 비교·분석하여 그 중 필요한 부분만 취사선택하는 과정이 결국 ‘나만의 풀이’를 만드는 핵심입니다. 단순히 남의 풀이를 그대로 받아들이는 것은 실력 향상에 큰 도움이 되지 않습니다.이번 문제는 기존 캔틸레버 구조물이 아닌, 단순보에서의 변단면 응용 문제입니다. 실제 하프 모의고사로 출제했을 당시, 많은 수강생들이 처음에는 ‘이게 과연 손으로 빠르게 풀 수 있는 문제인가’라는 의문을 가졌습니다. 그러나 처짐각법을 일관된 관점으로 적용하는 방법을 익힌 이후에는, 오히려 직관적으로..

1.개요마 전 한국도로공사 토목직 필기시험에서 변단면 처짐 문제가 출제되었다는 이야기를 듣고, 이를 응용하여 구성해 보았습니다.물론 이 문제는 M/EI 도의 1차 모멘트 비율을 이용해서도 충분히 처리할 수 있습니다.하지만 만약 문제에서 처짐을 직접 구하라고 한다면, 여러분은 어떤 방식으로 접근하실 것인지 한번 고민해 보셨으면 합니다.많은 분들이 중첩법을 활용하여 구하는 방법에 익숙하실 것 같습니다.이는 많은 분들이 이미 알고 있는 풀이여서 다른 방법을 소개하고자 합니다.바로 처짐각법을 활용하여 문제를 해결하는 과정을 다뤄보겠습니다.참고로 저는 이전에 처짐각법 시리즈를 통해 기본 이론을 정리한 바 있습니다.https://oreostructure.tistory.com/48 보 구조물 변위법의 기본 - 처짐각..

1. 개요문제를 보고 “아름답다”라고 느끼는 순간이 있습니다.그럴 때는 대부분, 다른 사람들은 복잡하게 돌아가는 길을 택할 때 출제자가 던져준 힌트를 통해 훨씬 쉽고 간결하게 해결할 수 있을 때입니다.특히 2024년 5급 응용역학 3번 문제는 그런 사례라고 생각합니다.3번의 1번과 2번을 각각 별개의 문제로 풀어내는 경우도 많지만, 사실 2번은 1번의 결과를 활용하면 매우 간결하게 해결할 수 있습니다.출제자는 1번에서 ‘단위 회전각’을 제시함으로써 변위법 적용에 대한 힌트를 명확히 주고 있습니다.이 힌트를 제대로 읽어낸다면, 3차 부정정 구조인 2번 문제도 단자유도 문제로 환원하여 쉽고 깔끔하게 풀 수 있습니다.이 지점에서 출제자의 의도를 느끼게 됩니다.단순히 계산 능력이 아니라, 변위법을 이해하고 이를..

1.개요캔틸레버의 자유단에서 집중하중이 발생하였을때 처짐과 회전각의 관계에 대해 암기하고 계시는 분들이 많을 것이라 생각합니다.해당 공식을 보고 있으면 처짐과 처짐각 사이에 흥미로운 관계가 있음을 알 수 있습니다.위와같은 관계는 기본공식을 자주 활용하고 연습하던 분들은 쉽게 확인할 수 있는 사실입니다.제가 출제한 모의고사 2회차의 12번 문제는 이와 같은 관계를 활용할 수 있는지에 대해 묻는 질문이었습니다.이제 문제를 풀어보겠습니다.2. 문제 풀이 (실전용)위의 관계를 살펴보면 자유단(모멘트가 0이며 수직 처짐이 존재)하는 곳에서의 회전각은 처짐량에 비례하며 부재 길이에 반비례함을 알 수 있습니다.구조물이 B점의 수직처짐 (δ)이 동일하기 때문에 회전각 θ는 부재의 길이 L에 반비례하게 됩니다.따라서 문..

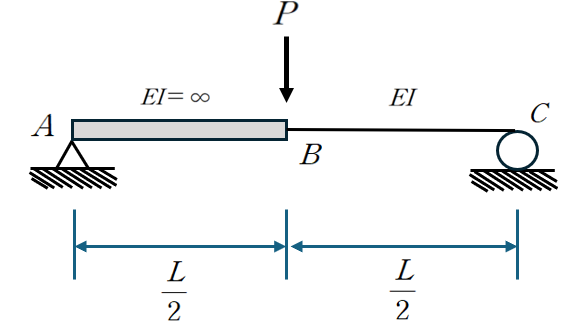
1.개요위 문제에서 분포하중이 삼각형이 아니라 등분포하중이라면,등분포하중을 받는 캔틸레버 처짐 공식을 활용하여변위일치법으로도 충분히 풀이가 가능합니다.하지만 여기서 한 단계 더 생각해보면, 만약 분포하중이 아니라 B점에 집중하중이 작용한다면문제는 훨씬 더 간단해집니다. 이와 같은 사고의 흐름은 매우 정상적이며,“어떻게 하면 더 쉽게 풀 수 있을까?”라는 열망에서 출발한 것입니다.구조물과 하중을 있는 그대로 받아들이는 것이 아니라,더 단순한 형태로 치환해서 바라볼 수 있는 관점을 갖게 되면문제 풀이 능력은 급격히 강력해집니다.이러한 생각의 흐름에 공감하신다면,제 블로그에서 다루고 있는 변위법 중심의 풀이들을 꼭 학습해 보시기 바랍니다.이때 추가로 반드시 짚고 넘어가야 할 것이FEM(고정단 모멘트)과 등가절..

1.개요위의 문제를 보고 어떤 생각이 드시나요?아마도 ‘굽힘에너지’라는 단어가 눈에 들어오는 순간, 대부분은 멈추지 못하고 앞으로 나아갈 것입니다.평형방정식을 세우고, 구간별 모멘트 식을 만들고,시간이 흘러가는 것을 느끼면서도 “여기까지 왔는데 멈춰야 하나?”를 고민하겠죠.하지만 이미 세운 식이 아까워 더 가는 분들도 있을 겁니다.그러다 모멘트 제곱항을 전개하면서 또 한 번 고민합니다.“이걸 정말 해야 하나?”이윽고 제곱꼴로 나온 2차식을 정적분하기 위해 세제곱 항을 처리하며, 마음속으로 기도하게 됩니다.제발… 이렇게나 열심히 풀고있는데... 계산 실수만은 나오지 않게 해주세요... 아멘. 벌써 2문제나 풀 수 있는 시간을 쏟았나이다... 여기서 돌아갈 수 없습니다...자, 여기서 질문 하나 드리겠습니다..