
1.개요
위 문제에서 분포하중이 삼각형이 아니라 등분포하중이라면,
등분포하중을 받는 캔틸레버 처짐 공식을 활용하여
변위일치법으로도 충분히 풀이가 가능합니다.
하지만 여기서 한 단계 더 생각해보면, 만약 분포하중이 아니라 B점에 집중하중이 작용한다면
문제는 훨씬 더 간단해집니다.
이와 같은 사고의 흐름은 매우 정상적이며,
“어떻게 하면 더 쉽게 풀 수 있을까?”라는 열망에서 출발한 것입니다.
구조물과 하중을 있는 그대로 받아들이는 것이 아니라,
더 단순한 형태로 치환해서 바라볼 수 있는 관점을 갖게 되면
문제 풀이 능력은 급격히 강력해집니다.
이러한 생각의 흐름에 공감하신다면,
제 블로그에서 다루고 있는 변위법 중심의 풀이들을 꼭 학습해 보시기 바랍니다.
이때 추가로 반드시 짚고 넘어가야 할 것이
FEM(고정단 모멘트)과 등가절점하중 개념입니다.
이는 변위법 풀이의 핵심 도구이며,
반드시 암기해야 할 5개의 대표 Case는 이미 별도의 포스팅으로 정리해 두었습니다.
해당 내용을 함께 참고하시면서
문제를 더 빠르고, 더 안정적으로 풀어내는 감각을 키워보시기 바랍니다.
https://oreostructure.tistory.com/131
FEM 공식 유도 및 응용 (Ⅱ)
https://oreostructure.com/130 FEM 공식 유도 및 응용 (Ⅰ)안녕하세요. 오레오 구조입니다.이번 포스팅에서는 필수적으로 알아두어야 할 FEM(Fixed End Moment) 공식 몇 가지를 직접 유도해 보고,이를 실제 문제
oreostructure.com
2.문제풀이
등가하중 산정을 위해 B의 모멘트 부분을 0으로 만들어 반대편으로 Carry Over 한 후, 모멘트 불균형에 따른 Shear와
단순보 모델링을 통한 전단력 효과를 더해주면 등가절점하중이 쉽게 산정됩니다.

따라서 문제를 다음과 같이 치환할 수 있습니다.
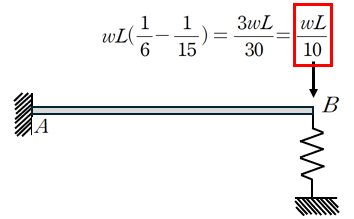
이제 문제는 매우 쉬워졌습니다.
병렬연결에 따른 전체 강성은 다음과 같습니다.
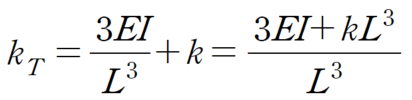
따라서 처짐은 등가절점하중에 전체 강성도를 나눠주면 간단하게 산정됩니다.

따라서 답은 ④번 입니다.
3.마무리하며
구조물을 간단하게 치환하고, 하중을 단순한 형태로 바꾸어 생각하는 것은
공무원 시험에 매우 적합한 전략이라고 생각합니다.
공학용 계산기를 자유롭게 활용하고 손계산 비중이 낮은
구조기술사나 5급 공채 시험에서는 크게 필요하지 않을 수 있습니다.
하지만 7급·9급 시험에서는 이 전략을 활용하면
문제를 훨씬 빠르고 정확하게 풀어나갈 수 있습니다.
이처럼 빠르게 치환하며 사고하기 위해서는 변위법적인 개념이 필수적입니다.
오는 2월 11일(수) 오후 8시,
휨부재를 중심으로 한 변위법 무료 특강을 진행합니다.
이번 특강에서 다루는 내용은
단순한 보 문제에 그치지 않고,
향후 합성구조물이나 복합 구조 해석에도 폭넓게 활용할 수 있는 기반이 됩니다.
시간이 되시는 분들은
신청하셔서 꼭 한 번 들어보시기를 추천드립니다.
[무료강의] 처짐각법 강의, 휨부재의 변위법 접근
안녕하세요. 오레오구조입니다.이전에 축부재를 주제로 한 변위법 특강을 진행한 바 있으며, 당시 참여해 주신 분들로부터 강의 내용과 구성에 대해 만족도가 높았다는 피드백을 받았습니다.
oreostructure.com
'재미있는 문제- 쉬운풀이 > 합성구조물' 카테고리의 다른 글
| 2009년 국가직 7급 18번 (강성도의 정의를 활용한 깔끔한 문제) (0) | 2025.12.05 |
|---|---|
| 2018년 국가직 7급 20번 (직렬 병렬 연결을 좋아하는 출제자들) (0) | 2025.11.09 |
| 2025년 5급 공채 응용역학 1번 문제 (2) | 2025.11.01 |
| 2017년 7급 국가직 7번 (하중을 강성도 비율로 나누어 갖는 병렬연결) (10) | 2025.10.29 |
| 2017년 7급 국가직 9번 문제 (출제자의 직렬 연결에 대한 힌트) (2) | 2025.10.28 |