
1. 개요
병렬 연결 문제로의 직관
최근 연달아 게시한 글들의 주제는 모두 직렬 연결과 병렬 연결의 개념을 다루고 있습니다.
이제 위의 문제를 보면, 자연스럽게 “이건 병렬 연결 문제구나” 하는 느낌이 오시나요?
이번 문제 역시 그 연장선상에 있습니다.
점 B에서의 수직 처짐은 AB 캔틸레버 부재와 BC 축부재에 동시에 영향을 미칩니다.
즉, B점의 처짐에 대해 두 부재가 함께 저항하므로
이 구조는 명확히 병렬 연결(parallel connection) 형태에 해당합니다.
문제 단순화 전략
문제를 보다 간단히 풀기 위해,
AB 부재의 등분포하중을 등가 격점하중(equivalent nodal load) 으로 치환하여 다루겠습니다.
이렇게 하면 하중이 절점에 집중된 형태로 바뀌어
병렬 연결 관계를 더 명확히 파악할 수 있고,
계산 또한 훨씬 간단해집니다.
2. 등가 격점하중의 개념
외력이 존재하지 않더라도, 온도 변화는 구조물에 내부 변형을 유발하는 간접적인 외력으로 작용할 수 있습니다.
이때 우리는 이러한 효과를 등가 격점하중(equivalent nodal load) 으로 치환하여 해석합니다.
등가 격점하중이란,
절점(node)에서 동일한 처짐을 유발하도록 작용하는 가상의 외력을 의미합니다.
즉, 실제 하중 대신 절점에 이 하중을 작용시켜도
결과적으로 구조물의 처짐이 같게 되는 개념입니다.
등가 격점하중은 구조물의 고정단 하중과 크기는 같고, 부호는 반대입니다.
즉, 고정단이 구조물을 막아주던 힘을
이제 외력 형태로 “풀어준다”고 생각하면 됩니다.
3. 캔틸레버 보에서 등가 격점하중 산정
등분포 Beam에서의 FEM (Fixed End Moment)은 다음과 같이 표현 가능합니다.
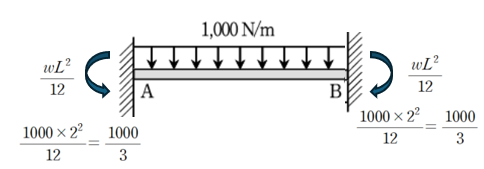
한편 B점은 모멘트가 0이므로 외력으로 동일하지만 부호 반대의 힘을 가합니다. 그리고 이를 반대편으로 절반만큼 carry over 시켜줍니다. (모멘트 분배법 개념)
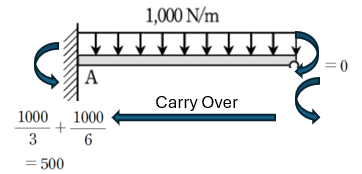
1000N/m의 등분포 하중은 다음과 같이 등가 격점하중으로 변경되었습니다.
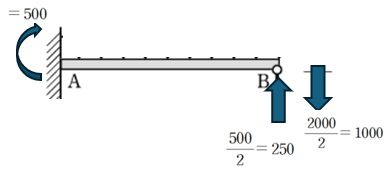
B점에서 1000N 등분포를 절반씩 나눠 갖고 모멘트 500에 대한 shear 균형까지 하여 B지점에서 등가 격점하중은 750으로 연직 하향으로 작용하는 것을 알 수 있습니다.
4. 구조물 병렬연결
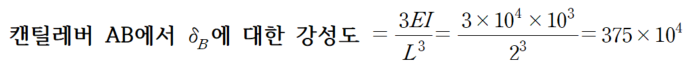

따라서

5. 마무리 하며
강성이 무한한 축부재의 거동
만약 축부재의 강성(stiffness) 이 무한대(∞) 라면 어떻게 될까요?
강성이 유한한 부재와 무한한 부재가 병렬로 존재할 때,
전체 하중은 항상 강성이 무한한 부재로 집중됩니다.
이는 단순한 비유로 보자면,
“하중은 변형이 가장 적은(거의 없는) 경로로 흐른다”는 원리 때문입니다.
따라서 축부재의 강성이 무한이라면,
그 부재는 변형하지 않으면서 모든 하중을 받아내는 형태가 됩니다.
이러한 상황은 실제 구조물에서 힌지(hinge) 나 롤러(roller) 지점과 동일하게 해석됩니다.
즉, 힌지나 롤러 위에 직접 하중이 작용하면,
그 지점이 하중 전체를 받아내며
다른 부재로는 하중이 전달되지 않습니다.
'재미있는 문제- 쉬운풀이 > 합성구조물' 카테고리의 다른 글
| 2009년 국가직 7급 18번 (강성도의 정의를 활용한 깔끔한 문제) (0) | 2025.12.05 |
|---|---|
| 2018년 국가직 7급 20번 (직렬 병렬 연결을 좋아하는 출제자들) (0) | 2025.11.09 |
| 2025년 5급 공채 응용역학 1번 문제 (2) | 2025.11.01 |
| 2017년 7급 국가직 9번 문제 (출제자의 직렬 연결에 대한 힌트) (2) | 2025.10.28 |
| 2017년 7급 국가직 17번 - 합성구조물의 스프링 치환 (4) | 2025.10.26 |