
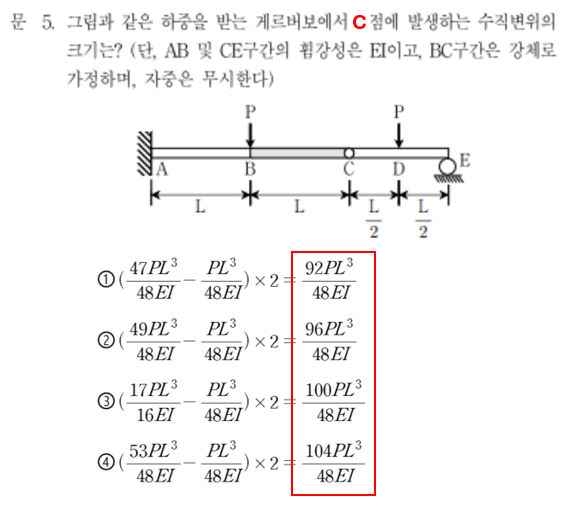
1. 개요
강체(EI=∞)가 문제에 등장했을 때의 감각
문제를 많이 풀다 보면, EI가 무한인 강체가 등장할 때 느껴야 하는 감각이 생깁니다.
첫째, 문제가 오히려 단순해집니다.
강체는 휨 변형이 없기 때문에 여러 절점의 움직임이 서로 묶이며,
많은 종속 자유도를 만들어 냅니다.
즉, 기구학적(Kinematic) 관계를 세우기가 훨씬 쉬워집니다.
둘째, 처짐을 구할 때 큰 도움이 됩니다.
EI가 무한이면, 휨에 의한 변형에너지는 존재할 수 없습니다.
따라서 강체 구간의 처짐은 단순히 각도 × 길이로 계산할 수 있습니다.
이를 모멘트 면적법 관점에서 보면,
M/EI 도식에서 EI=∞ 인 부분의 면적은 0이 됩니다.
즉, 이전 구간(M/EI ≠ 0)에서 생긴 회전각(θ)에 그 지점까지의 길이(모멘트 암)을 곱하면
그 값이 바로 처짐이 되는 것입니다.
결론적으로, 휨문제에서 강체는 복잡한 요소가 아니라
오히려 문제를 단순화시키는 ‘도움 장치’로 보는 것이 좋습니다.
해당 문제와 함께 2017년 국가직 응용역학 15번 (EI 무한 강체)도 함께 비교하여 보시면 좋습니다.
2017년 7급 국가직 응용역학 15번 문제
이번 문제는 세 가지 방법으로 접근해 보겠습니다.① 최소일의 원리② 처짐각법③ 모멘트 면적법세 방법 모두 손계산으로 충분히 풀 수 있는 수준이며,개인적으로는 이 문제에 대해서는 최소일
oreostructure.com
2. 문제의 핵심 포인트와 이를 통한 단순화
(1) 문제의 핵심 포인트 1
일반적으로 내부힌지가 존재한다면, 구조물을 그 힌지 위치를 기준으로 두 부분으로 분리하여 생각할 수 있습니다.
내부힌지에서는 다음과 같은 기구학적(Kinematic) 관계가 성립합니다.
- 수직 처짐은 양쪽에서 동일하다.
- 모멘트는 전달되지 않는다. (즉, 내부힌지에서 M = 0)
따라서, 각도(회전각)에 대한 적합조건은 고려할 필요가 없습니다.
힌지를 기준으로 좌우 부재가 서로 독립적으로 회전할 수 있기 때문입니다.
(2) 문제의 핵심 포인트 2
한편 D의 수직 처짐은 다음과 같이 표현 할 수 있습니다.

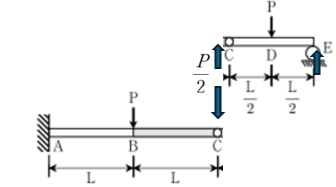
따라서 δc 를 찾는 것이 사실상 문제 푸는 것의 핵심이며 다음과 같이 문제를 변형해볼 수 있습니다.
(3) 문제의 핵심 포인트 3
구조물에서 CDE 부재는 점 C의 처짐(δc) 에 대해 아무런 강성(stiffness)을 제공하지 못합니다.
그 이유는 CDE가 단순보이기 때문입니다.
단순보는 양단 모멘트가 0이므로, 지점 침하가 발생하더라도 모멘트가 새로 생기지 않습니다.
즉, 지점의 처짐 변화가 있어도 그에 대한 저항 모멘트가 형성되지 않으므로
CDE 부재는 δc 방향으로 구조적 저항을 전혀 하지 않습니다.
만약 CDE가 E점을 고정단으로 하는 외팔보(Cantilever) 였다면, 이 부재는 병렬 스프링 시스템처럼 작용하여
C점 처짐에 강성을 부여했을 것입니다.
그러나 단순보 조건에서는 그렇지 않습니다.
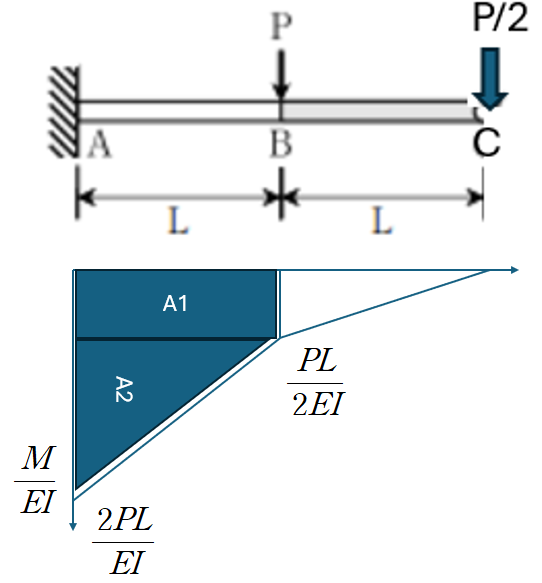
결국, 자유물체도 상에서 본다면, D점에 작용하는 하중 P의 절반인 P/2 만이 단순히 C점으로 전달될 뿐이며,
구조적으로 C점의 처짐을 제한하거나 저항하지는 않습니다.
따라서 문제를 다음과 같이 더 단순화 할 수 있습니다.

3. 간단한 문제 풀이
단순화된 구조물에서 C점의 처짐( δc ) 을 구하는 것은 생각보다 매우 간단합니다.
실제 시험에서는 자신에게 가장 익숙한 방법을 사용하는 것이 중요합니다.
공식을 외우는 것보다, 각 방법의 특징을 이해하고 상황에 맞게 적용하는 것이 훨씬 효율적입니다.
개인적으로는 이와 같은 캔틸레버 형태의 문제에서는 모멘트 면적법이나 중첩법(superposition method) 이
C점 처짐을 구하는 데 가장 직관적이고 빠르다고 생각합니다.
최소일 풀이를 전개할 계획이라면 카스틸리아노 2법칙 보다는 가상하중 1을 하여 손적분하는 것이 나아보입니다.
추가로, 조금 다른 접근으로, EI가 무한인 강체 부재의 회전에 의해 생기는 종속 변위 관계를 보여주기 위해
조금 비효율적일 수 있지만 처짐각법(slope-deflection method) 풀이도 함께 소개하겠습니다.
참고로 답은 ②번이 나온다.
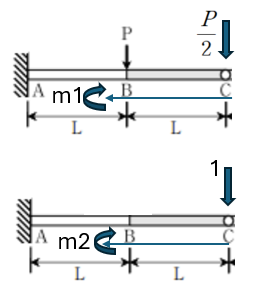
(1) 모멘트 면적법을 통한 δc 산정

(2) 중첩법을 통한 δc 산정


(3) 가상일의 법칙 (단위하중법)

(4) 처짐각법


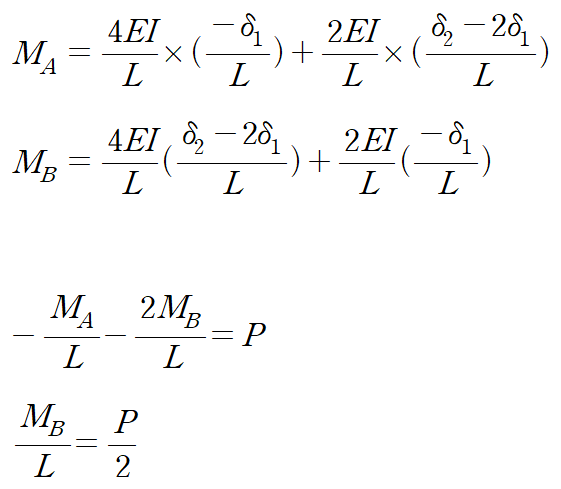

4. 마무리
이전에 다루었던 문제 역시 스프링 치환을 통해 구조물을 단순화한 예였습니다.
이번에는 한 단계 더 나아가, 수직방향 강성도가 없는 부재를 제거하고 그 하중만 옮겨서 강체가 포함된 캔틸레버 구조로 문제를 변환했습니다.
이처럼 구조물을 단순화하거나 형태를 변형할 때의 핵심은 자유도 산정과 변위법에 대한 정확한 이해에 있습니다.
이 두 가지 개념이 잡혀 있어야 복잡한 구조도 간단히 모델링할 수 있습니다.
앞으로 이 블로그에 올라오는 풀이 과정을 꾸준히 학습한다면, 자연스럽게 이러한 개념이 체계적으로 잡힐 것입니다.
일부 문제는 여러 가지 방법으로 의도적으로 풀이했습니다. 이는 독자 여러분이 시험장에서 사용할 자신만의 전략을 찾기 위함입니다. 어떤 방법은 자신에게 잘 맞아 실전용으로 쓸 수 있고, 다른 방법은 과감히 버려도 괜찮습니다.
다만 “버린다”는 것은 “잊는다”는 의미가 아닙니다.
그 과정에서 얻은 개념적 이해는 훗날 구조기술사 같은 상위 시험에 도전할 때 확실히 도움이 될 것입니다.
**참고 : 강체가 포함된 캔틸레버의 Stiffness를 공식으로 외우는 경우도 있습니다.

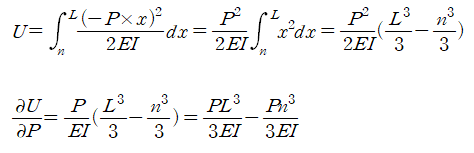
궁금해하는 분들을 위해 최소일의 원리(카스틸리아노 제2법칙) 으로
그 공식을 유도해보았지만, 개인적으로는 큰 의미를 두지 않습니다.
사람마다 접근 방식은 다르겠지만, 필요한 공식만 명확히 이해하고 있다면 추가로 더 많은 공식을 암기할 필요는 없습니다.
물론 당연한 얘기겠지만 모든 공식은 정확하게 외운다는 가정하에 외워서 나쁠 건 없습니다.
'재미있는 문제- 쉬운풀이 > 정정 보의 곡률, 처짐' 카테고리의 다른 글
| 2022년 9급 국가직 응용역학 개론 10번 - 보기를 통한 합리적 추론 기술 (0) | 2025.10.31 |
|---|---|
| 2024년 7급 국가직 17번 응용역학 문제 (등가 격점 하중의 활용) (1) | 2025.10.27 |
| 2017년 7급 국가직 응용역학 15번 문제 (0) | 2025.10.21 |
| 2025년 7급 응용역학 가형 23번 풀이 (0) | 2025.09.23 |
| 2025년 7급 응용역학 가형 22번 풀이 (0) | 2025.09.23 |