1. 개요
7급·9급 응용역학 시험에서는
단면2차모멘트, 극관성모멘트, 그리고 평행축 정리(Parallel Axis Theorem) 를 활용하는 문항이 매우 전형적으로 출제됩니다.
이를 위해서는 기본적인 단면 성질(section properties) 을 반드시 숙지하고 있어야 합니다.
구체적으로는 다음과 같은 값들을 평소에 자연스럽게 떠올릴 수 있을 정도로 익혀 두어야 합니다.
- 단면2차모멘트 I
- 극관성모멘트 J
- 형상계수(Shape Factor)
- 단면계수(Section Modulus)
- 소성단면계수(Plastic Section Modulus)
- 단면상승모멘트(Ixy)
- 대칭축에 따른 단면상승모멘트 특징 (대칭축 1개, 2개)
이 정도는 사실상 필수 암기 사항에 가깝습니다.
이제 이러한 개념들이 어떻게 활용되는지 확인하기 위해,
2015년 서울시 응용역학 2번 문제를 통해
전형적인 단면2차모멘트 계산과 평행축 정리 적용 과정을 함께 살펴보겠습니다.
2. 평행축 정리 에 대한 간단한 설명
본래 단면 2차 모멘트는 단면의 무게중심(Centroid, Center of Mass) 을 기준으로 정의됩니다.
무게중심을 기준으로 할 경우 단면의 1차 모멘트(Σ yᵢ Aᵢ) 는 0이 되므로,
단면의 2차 모멘트는 다음과 같이 표현됩니다.
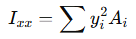
이때 거리 d 만큼 떨어진 축에서 단면의 2차 모멘트를 산정한다고 가정하게 되면 다음과 같이 정리할 수 있습니다.
이제 기준축에서 거리 d 만큼 떨어진 또 다른 축에 대해
단면의 2차 모멘트를 구한다고 가정하면 다음과 같이 정리할 수 있습니다.
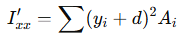
이를 전개 하면 다음과 같습니다.
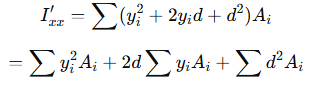
여기서
이고,
이므로
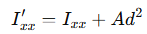
라는 결론에 도달하게 됩니다.
따라서, 평행축 정리(Parallel Axis Theorem) 는
“단면적 × 거리²만큼 단면 2차 모멘트가 증가한다”는 매우 직관적인 의미를 가집니다.
즉, 축에서 멀어질수록 단면의 강성(2차 모멘트)은 크게 증가하게 됩니다.
3. 문제 풀이
원의 중심에 대한 단면 2차 모멘트는 다음과 같습니다.
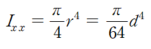
유도 과정은 다음과 같으나, 7급 9급 시험 준비 수험생분들께선 유도과정은 참고로만 알아두시고 결과는 꼭 암기해두셔야 합니다.
단면의 중심으로 부터 떨어진 거리는 r 이며 평행축 정리를 적용시 단면 2차 모멘트는 다음과 같습니다.
따라서 답은 다음과 같이 산정됩니다.
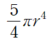
답은 ③번입니다.
4. 마무리 하며
문제 자체는 난이도로 분류하면 하(下) 에 속하지만,
평행축 정리(Parallel Axis Theorem) 는 매년 반복해서 등장하는 대표적인 단골 유형입니다.
꼭 기억하셔야 할 핵심은 다음 한 문장입니다.
“축에서 멀어질수록 단면 2차 모멘트는 단면적 × 거리² 만큼 증가한다.”
즉, 거리가 조금만 증가해도 2차 모멘트는 제곱 비례로 크게 커지므로
단면 강성 해석에서 결정적인 역할을 하게 됩니다.
토목·건축 관련 시험을 준비하시는 분들은
단면 2차 모멘트는 반드시 암기해 두셔야 하는 기본기입니다.
특히 자주 등장하는 다음 단면들은 무조건 외워두어야 합니다.
- 사각형 단면
- 삼각형 단면
- 원형 단면
- 원형 중공단면
또한 글의 개요에서 언급드린 것처럼,
단면 성질(section properties) 은 수첩 혹은 노트에 따로 정리해두고
꾸준히 암기하시는 것을 strongly 권장드립니다.
시험장에서 이를 다시 유도할 시간은 없습니다.
그리고 단면 관련 문항은 많은 수험생들이 이미 값을 암기하고 있는 영역이므로
정답률이 매우 높은 편입니다.
즉, 이 파트의 기본기를 정리해 두는 것만으로도
전체 점수 안정성에 큰 도움이 됩니다.