Insight 구조&응용역학

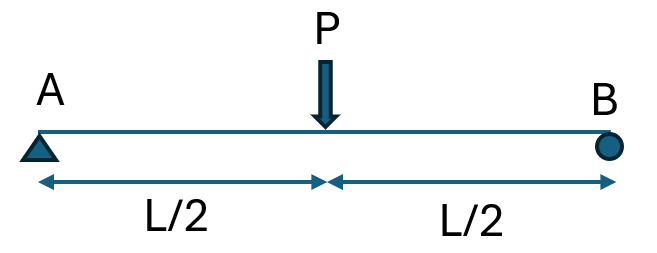
1. 개요(1) 등가 절점하중(Equivalent Nodal Force)의 개념구조역학을 공부하다 보면 “등가 절점하중(또는 등가 격점하중)”이라는 개념이 자주 등장합니다.이 용어는 단순히 수식의 변환이 아니라, 전산 구조해석의 핵심 개념 중 하나입니다.이번 글에서는“단순보 정중앙에 집중하중이 작용할 때, 양 끝단의 회전량을 구하시오.”라는 간단한 예제를 통해 등가 절점하중이 왜 필요한지, 그리고 어떻게 쓰이는지 살펴보겠습니다.(2) 전산 구조해석의 기본 관점 — Node 중심 사고현대의 구조해석 프로그램(FEM, Frame Analysis 등)은 대부분 ‘절점(Node)’ 중심으로 사고합니다.즉, 부재(Element) 내부에서 어떤 변형이 일어나더라도,그 결과를 절점에서의 힘과 변위로 환산하여 해석합니..

1. 개요이번 문제를 공액보법(Conjugate Beam Method) 으로 푼다고 가정해 보겠습니다.먼저, 실제 보의 굽힘모멘트도(BMD) 를 산정한 뒤,이를 EI로 나누어 단순보에 작용하는 등가 하중으로 치환하는 과정을 거치게 됩니다.즉, M/EI 도를 단순보 위의 하중 분포로 바꾸는 것이 첫 단계입니다. 하지만 공액보법을 적용할 때 가장 시간이 소요되는 부분은바로 공액보의 반력 계산입니다.이를 일일이 적분하거나 모멘트 균형으로 구하면 복잡해지기 때문입니다.이때 유용한 방법이 바로 등가 하중(Equivalent Load) 을 이용하는 것입니다.공액보의 반력을 등가하중으로 빠르게 환산하면 복잡한 계산 과정을 상당히 단축할 수 있습니다. 특히, 단순보로 모델링했을 때 공액보의 반력은 실제 보의 회전량(θ..

1. 개요공식은 많이 외울수록 도움이 될 수 있지만, 그만큼 정확하게 기억하는 것이 중요합니다.만약 공식이 헷갈리거나 기억이 모호해진다면, 언제든지 빠르게 다시 유도할 수 있는 능력을 갖추는 것이 더 실질적인 실력이라고 생각합니다.이를 위해서는 기본적인 강성(Stiffness) 개념과 등가 격점하중(Equivalent Nodal Load) 의 활용법을 확실히 익혀두는 것이 좋습니다. 대부분의 교재나 참고서에서는 공액보법(Conjugate Beam Method) 이나 모멘트 면적법(Moment-Area Method) 을 이용해 처짐을 계산하지만,저는 앞으로 처짐각법(Slope-Deflection Method) 과가상변위의 법칙(Virtual Work Principle) 에 기반한 변위법(Displaceme..

1.개요https://oreostructure.tistory.com/31 2024년 7급 국가직 응용역학 풀이 (스마트한 풀이는 실수를 줄인다.)총평2024년 7급 국가직 응용역학 시험은 일부 계산을 요구하는 문항이 있었지만, 전반적으로 많은 연산이 필요한 편은 아니었다.7급의 난점은 “문제 자체의 난도”보다 “한정된 시간 안에 손계oreostructure.com최근 게시한 2024년도 7급 응용역학 풀이 중 17번 문항에서 계산상의 오류가 포함된 채 포스팅된 것을 확인했습니다.다행히 한 구독자분께서 세심하게 지적해주셔서 문제를 빠르게 발견하고 수정할 수 있었습니다.이 자리를 빌려 감사의 말씀을 드립니다. 사과의 뜻을 전함과 동시에, 해당 문항에 대한 이해를 돕기 위해이번에는 등가 격점하중(Equival..

2024년 7급 군무원 응용역학 기출 총평2024년 군무원 7급 응용역학 시험은 기본 개념을 묻는 문제와 계산량이 많은 문제의 구분이 명확했다.시간 안배와 선택적 접근이 중요했으며, 어려운 문제를 붙잡기보다는 반드시 맞춰야 하는 문제에서 점수를 확보하는 것이 핵심이었다.난이도는 어려운 편이다.반드시 맞춰야 하는 문제2, 3, 4, 7, 12, 13, 14, 15, 18, 21, 22, 24, 25이 구간의 문제들은 난이도가 낮고 기출 유형과 유사했다.기본 공식 암기와 계산 숙련도가 있으면 빠르게 정답을 찾을 수 있었다.시간은 조금 걸리지만 풀만한 문제16, 19 ,20어색한 유형이지만 효율적 접근법통해 풀만했다.19번의 경우 K트러스 단면법을 학습하였다면 매우 쉬운 유형으로 분류된다.시간이 막대하게 걸리..