
1. 개요
공식은 많이 외울수록 도움이 될 수 있지만, 그만큼 정확하게 기억하는 것이 중요합니다.
만약 공식이 헷갈리거나 기억이 모호해진다면, 언제든지 빠르게 다시 유도할 수 있는 능력을 갖추는 것이 더 실질적인 실력이라고 생각합니다.
이를 위해서는 기본적인 강성(Stiffness) 개념과 등가 격점하중(Equivalent Nodal Load) 의 활용법을 확실히 익혀두는 것이 좋습니다. 대부분의 교재나 참고서에서는 공액보법(Conjugate Beam Method) 이나 모멘트 면적법(Moment-Area Method) 을 이용해 처짐을 계산하지만,
저는 앞으로 처짐각법(Slope-Deflection Method) 과
가상변위의 법칙(Virtual Work Principle) 에 기반한 변위법(Displacement Method) 으로 유도하여,
응용역학과 구조역학을 조금 다른 관점에서 이해할 수 있도록 안내드리고자 합니다.
2. 단순보 중앙 처짐
단순보 중앙에 집중하중이 작용할 때의 처짐 공식은,
토목 및 구조 관련 시험을 준비하시는 분들이 절대 잊어서는 안 되는 기본 공식 중 하나입니다.
만약 이 공식을 순간적으로 기억하지 못하더라도, 변위법(Displacement Method) 의 개념을 이해하고 있다면
그 이론을 바탕으로 빠르게 처짐을 유도할 수 있습니다.
이번에는 그러한 상황을 가정하여,
공식을 외우지 않은 상태에서 단순보 중앙 처짐을 직접 유도하는 과정을 함께 살펴보겠습니다.

(1) 대칭구조물-대칭 하중에 대한 모델링 및 강성도 산정

대칭 축을 기점으로 Fixed-roller로 모델링이 가능하며 가상의 변위 δ를 주어 가상 변위의 법칙을 활용하면 다음과 같습니다.

따라서 반쪽 구조물에 대한 강성도는 24EI/L^3 이 됩니다.

중앙 처짐 δ에 대해 두개의 구조물이 병렬연결로서 저항을 하고 있기 때문에 전체 강성도는 다음과 같습니다.
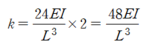
따라서 하중이 가해지는 중앙부의 처짐은 다음과 같이 산정됩니다.
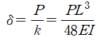
3. 고정단-고정단에서 집중하중에 의한 중앙 처짐

(1) 대칭구조물-대칭 하중에 대한 모델링 및 강성도 산정

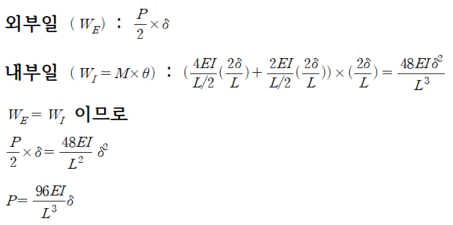
따라서 반쪽 구조물에 대한 강성도는 96EI/L^3 이 됩니다.
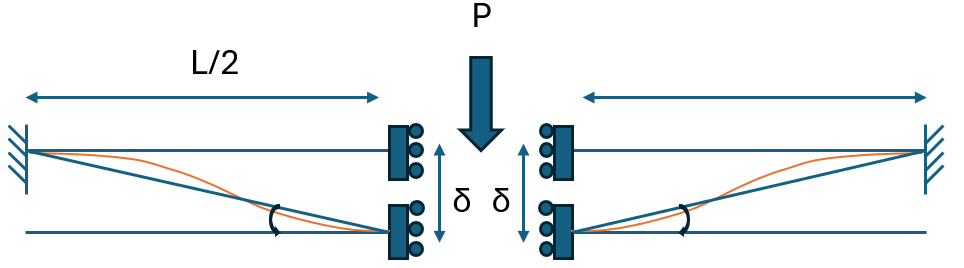
중앙 처짐 δ에 대해 두개의 구조물이 병렬연결로서 저항을 하고 있기 때문에 전체 강성도는 다음과 같습니다.
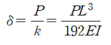
4. 등분포 하중일때의 중앙부 처짐
등분포 즉, 절점 (node)에 걸리지 않은 하중은 해당 절점의 처짐을 동일하게 만드는 등가 절점 하중으로 치환하여 해석하면 편리합니다.

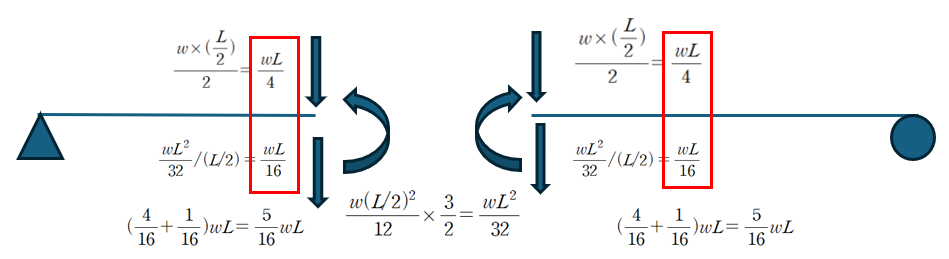
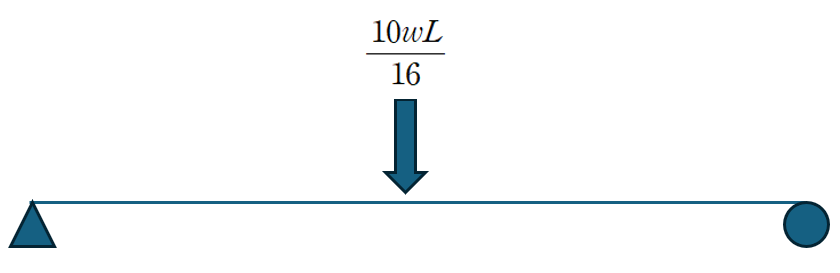
따라서 중앙부에 10wL/16이라는 집중하중이 작용하는것과 동일한 처짐결과를 얻게 됩니다.

5. 고정단-고정단에서 등분포 하중에 의한 중앙 처짐
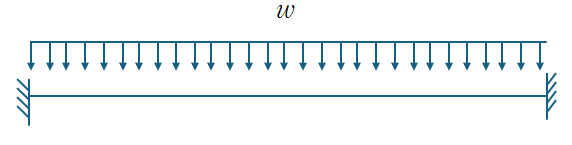
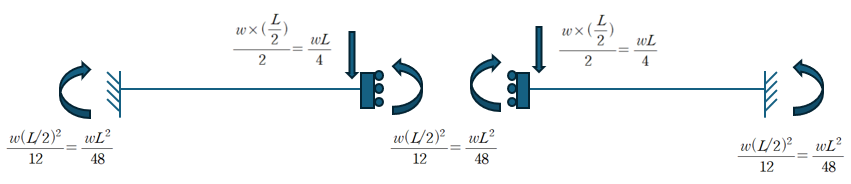
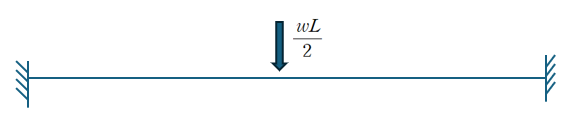
따라서 중앙부에 wL/2이라는 집중하중이 작용하는것과 동일한 처짐결과를 얻게 됩니다.

6. 마무리 하며
2025년 서울시 7급 16번에 대한 문제의 보기와 답은 아래의 링크를 참조하시기 바랍니다.
https://oreostructure.tistory.com/51
2025년 7급 서울시 응용역학 풀이 (유연도와 강성도에 익숙해지자)
“바로 풀린다” 리스트 (문제당 30초 내외)1, 2, 3, 6 (부재의 부피 산정 매우 간단), 7(보기 활용), 9 (출제자의 배려), 10 (보기 활용)11 (변위일치 공식을 알려줌), 13(전형적인 유형), 14 (가상일의 원
oreostructure.com
이번 포스팅의 핵심 주제는
변위법(가상변위의 법칙, 처짐각법) 을 이용해
보 구조의 중앙 처짐을 빠르고 직관적으로 구할 수 있다는 점입니다.
앞으로도 이러한 접근을 통해
기본적인 강성도(Stiffness) 와
다양한 하중 조건에서의 등가 격점하중(Equivalent Nodal Load) 을
더 쉽게 이해하고 계산하는 데 도움이 되시길 바랍니다.
'재미있는 문제- 쉬운풀이 > 부정정 보의 해석' 카테고리의 다른 글
| 2026년 7급 근로감독 산업안전 응용역학 23번 (변위법적인 쉬운 접근) (0) | 2026.01.26 |
|---|---|
| 2019년 7급 국가직 응용역학 10번 (부정정 보 처짐의 쉬운 풀이) (0) | 2026.01.20 |
| 2009년 7급 국가직 응용역학 5번 문제 (변위 기반의 생각) (0) | 2025.12.06 |
| 2015년 7급 서울시 응용역학 10번 (해답을 넘은 해설 : 영향선과 FEM) (0) | 2025.11.26 |
| 2015년 7급 서울시 응용역학 5번 (부정보의 지점침하) (2) | 2025.11.16 |