
1. 개요
이번 문제를 공액보법(Conjugate Beam Method) 으로 푼다고 가정해 보겠습니다.
먼저, 실제 보의 굽힘모멘트도(BMD) 를 산정한 뒤,
이를 EI로 나누어 단순보에 작용하는 등가 하중으로 치환하는 과정을 거치게 됩니다.
즉, M/EI 도를 단순보 위의 하중 분포로 바꾸는 것이 첫 단계입니다.
하지만 공액보법을 적용할 때 가장 시간이 소요되는 부분은
바로 공액보의 반력 계산입니다.
이를 일일이 적분하거나 모멘트 균형으로 구하면 복잡해지기 때문입니다.
이때 유용한 방법이 바로 등가 하중(Equivalent Load) 을 이용하는 것입니다.
공액보의 반력을 등가하중으로 빠르게 환산하면 복잡한 계산 과정을 상당히 단축할 수 있습니다.
특히, 단순보로 모델링했을 때 공액보의 반력은 실제 보의 회전량(θ) 에 대응하므로,
이를 등가 격점하중(Equivalent Nodal Load) 개념과 유연도(Flexibility) 관계로 표현하면
의미상으로도 동일하며, 훨씬 간단하게 산정할 수 있습니다.
[참고] 2025년 서울시 7급 문제풀이는 아래 링크에서 확인할 수 있습니다.
2025년 7급 서울시 응용역학 풀이 (유연도와 강성도에 익숙해지자)
“바로 풀린다” 리스트 (문제당 30초 내외)1, 2, 3, 6 (부재의 부피 산정 매우 간단), 7(보기 활용), 9 (출제자의 배려), 10 (보기 활용)11 (변위일치 공식을 알려줌), 13(전형적인 유형), 14 (가상일의 원
oreostructure.com
2. 빠른 풀이 (등가 결점 하중 + 공액보)
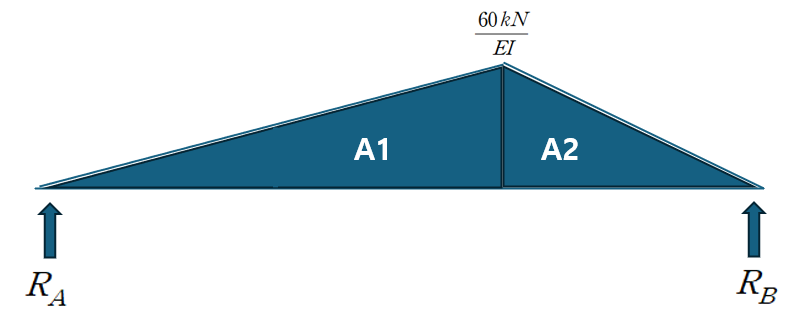
(1) 공액보법을 활용하되, 반력은 등가 격점 하중을 활용하여 산정하였습니다.

(2) B에서의 처짐각 구하기 위해 삼각형 닮음 활용(1:2 닮음 → 넓이 1:4 닮음), 공액보의 B에서의 전단 산정 (시계방향 +)

(3) EI 대입
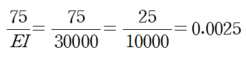
기존 공액보법만 활용하였을때와 비교해보시면 확연하게 풀이가 줄어들었음을 알 수 있을 겁니다.
가장 큰 시간 단축은 절점에서의 회전량 (즉, 공액법의 반력)을 빠르게 산정한 것에 있습니다.
다음은 공액보를 활용하였을때와 등가 격점 하중을 활용하였을 때를 비교하여 설명드리겠습니다.
3. 공액보를 위한 BMD
(1) 반력 산정
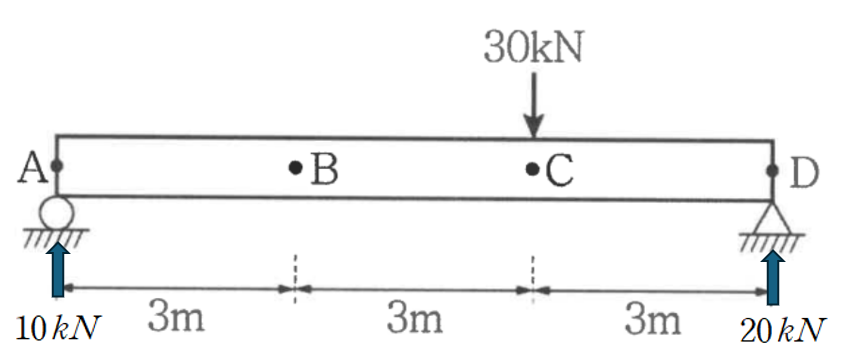
(2) M/EI 도 산정

(3) 전통적 공액보법 방식으로 양끝단 회전량 산정
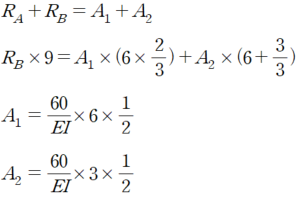
전통적 공액보법 방식을 활용시 위의 연립방정식을 풀어야 한다는 고통이 있습니다.
사람마다 다를 수 있겠지만 일반적으로 시험장에서는 연립방정식 푸는 것을 최소화 하면 도움이 된다고 생각합니다.
위의 공식에서 RB를 구하여 대입법으로 RA를 산정하면 다음과 같습니다.

3. 등가 격점하중을 활용한 양끝단 회전량 산정
(1) 고정단 모멘트 (암기 사항)
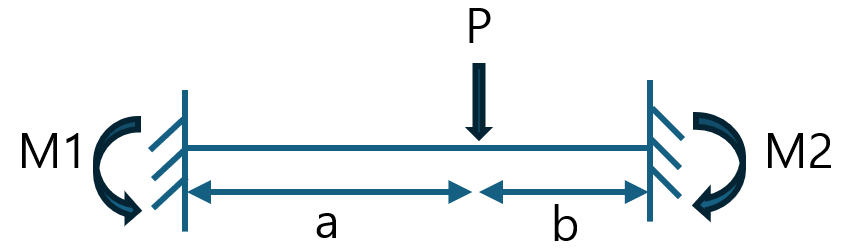

(2) 등가 격점하중을 통한 양 끝단 회전량 산정


(3) 장점
등가 격점하중을 활용시 고정단 모멘트를 암기해야 하는 단점이 있지만 다음과 같은 장점이 있습니다.
- 연립방정식을 풀 필요가 없습니다.
- BMD를 그릴 필요가 없습니다.
- 연립방정식을 풀지 않으므로 시험장에서 빠르고 실수없이 풀 가능성이 커집니다.
4. 마무리하며
저는 7급·9급 응용역학 시험 문제 풀이에서 등가 격점하중(Equivalent Nodal Load)을 활용하는 것이 가장 효율적이라고 믿고 있습니다.
수험생분들께서 어떻게 생각하실지는 모르겠지만, 시중 문제집이나 인터넷 해설, 유튜브 강의 등을 살펴보면
이 개념을 활용한 풀이가 거의 없다는 점이 늘 아쉽게 느껴집니다.
물론, 연립방정식을 활용한 정석적인 풀이 방식도 효율적일 수 있습니다.
하지만 그것은 집에서 충분히 여유 있는 시간과 안정된 마음으로 공부할 때 실수없이 가볍게 풀립니다.
실제 시험장에서는 심장이 뛰고, 시간에 쫓기며, 손이 떨리는 상황 속에서
복잡한 계산 과정이 오히려 실수로 이어질 때가 많습니다.
따라서 “이 문제는 내가 풀 수 있다”에서 멈추지 말고,
“어떻게 하면 더 빠르고 효율적으로 풀 수 있을까?” 를 끊임없이 고민하는 자세가 필요합니다.
그 사고의 출발점이 바로 등가 격점하중을 이용한 간결한 해석 접근법이라 생각합니다.
'재미있는 문제- 쉬운풀이 > 정정 보의 곡률, 처짐' 카테고리의 다른 글
| 2015년 7급 서울시 응용역학 7번 (보부재의 온도 변화 처리) (0) | 2025.11.16 |
|---|---|
| 2025년 7급 응용역학 가형 22번 풀이 (공액보법으로 푸는 방법) (0) | 2025.11.11 |
| 2022년 9급 국가직 응용역학 개론 10번 - 보기를 통한 합리적 추론 기술 (0) | 2025.10.31 |
| 2024년 7급 국가직 17번 응용역학 문제 (등가 격점 하중의 활용) (1) | 2025.10.27 |
| 2018년 7급 국가직 응용역학 5번 (EI+강체 유형을 접근하는 여러 방식) (0) | 2025.10.27 |