
1. 개요
위 문제는 온도 변화에 따라 보 부재에 발생하는 곡률(Curvature) 을 묻는 유형입니다.
여기서 한 가지 중요한 포인트가 있습니다.
혹시 보 부재의 온도 조건과 일반 축부재의 온도 조건의 차이점을 눈치채셨나요?
공무원·공기업·기사 시험에서 온도 조건이 주어질 때,
- 축부재는 단면 전체에 동일한(균일한) 온도 변화 ΔT를 줍니다.
- 보 부재는 단면의 상·하섬유에 서로 다른 온도 변화(ΔT 상, ΔT 하)를 줍니다.
이 차이가 발생 이유는 다음과 같습니다.
✔ 축부재 (Bar)
축부재는 모멘트에 저항하지 않는 구조물입니다.
즉, 외력에 대해 축력(Axial Force) 으로만 저항합니다.
따라서 온도 변화가 주어질 경우에는
단면 전체에 동일한 온도 변화가 작용하며,

이렇게 단면 전체에 일정한 변형률이 생성될 뿐,
상·하단의 변형률 차이는 없기 때문에 곡률이 발생하지 않습니다.
✔ 보 부재 (Beam)
반면 보 부재는 휨(Bending) 으로 외력에 저항하는 구조물입니다.
따라서 온도가 가해질 때 단면 상하부의 온도 변화가 다르게 주어지면,
상·하섬유의 팽창율(변형률)이 달라지고,
- 위는 많이 늘어나고
- 아래는 적게 늘어나면
단면은 자연스럽게 휘어지게(곡률이 생기게) 됩니다.
즉,
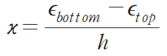
이와 같은 형태의 온도·변형률·곡률 관계가 성립합니다.
2. 문제풀이

(1) 단면의 변형률 분포

(2) 곡률 산정
변형률 차이에 따른 곡률(κ)은 다음과 같습니다.
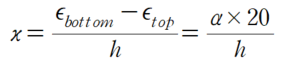

(3) 좌표축 유의
이때 좌표축 방향에 따른 부호를 반드시 확인해야 합니다.
그림을 보면, 곡률반경의 중심이 –y축 방향에 위치하고 있습니다.
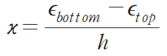
위의 방식으로 산정한 곡률이 양(+) 값이 되었을때,
- 만약 곡률반경 중심이 +y축 방향에 있다면 곡률 κ는 양(+) 값이 되고,
- 곡률반경 중심이 –y축 방향에 있으면 곡률 κ는 음(–) 값이 됩니다.
따라서 본 문제에서는 곡률의 크기는 위에서 구한 값과 같지만,
곡률반경이 –y 방향에 있으므로 부호는 –로 취해야 한다는 점을
꼭 함께 고려하셔야 합니다.


3. 마무리하며
따라서 답은 ④번이 됩니다.
이번 문제에서는 곡률(κ) 만을 계산하고 마무리했지만, 실제 시험에서는 이 개념을 다양한 방식으로 확장해 출제할 수 있습니다.
예를 들어,
- 특정 위치에서의 회전각(θ) 을 묻거나
- 단부 혹은 중간 지점에서의 처짐(y) 을 계산하게 할 수도 있습니다.
이럴 때는
- 곡률의 분포를 구한 뒤 공액보법을 적용하거나,
- 이중적분법을 사용하여 경계조건을 부여하면
손쉽게 각도와 처짐까지 계산할 수 있습니다.
온도에 따른 응력은 발생할까?
“온도 변화가 있었으니 응력이 생기는가?” 라는 질문이 있을 수 있습니다.
정답은 전혀 그렇지 않다 입니다.
그 이유는 다음 두 가지로 명확하게 설명할 수 있습니다.
- 정정(Statically Determinate) 구조물이다.
정정부재에서는 외적 구속이 없기 때문에, 온도로 인해 늘거나 줄어도
구조물이 저항하지 않으므로 응력이 발생하지 않습니다. - 온도가 단면 전체에 선형적으로 변화한다.
상부와 하부에 서로 다른 온도가 주어져도 변형률 분포가 선형이기 때문에
단면은 평면 변형(plane sections remain plane)을 그대로 유지합니다.
즉, 변형은 있지만 이를 막는 구속이 없으므로 응력은 생기지 않습니다.
문제는 난이도 ‘하(下)’지만, 사고는 ‘상(上)’으로 확장할 수 있다
비록 본 문항 자체는 쉬운 편에 속하지만,
곡률–기하학적 변형–응력 발생 조건–온도하중의 특성 등
다양한 개념으로 확장해 생각해볼 수 있는 좋은 문제입니다.
이러한 사고 확장은
7급·9급뿐 아니라
향후 구조기술사 준비에서도
매우 중요한 기반이 됩니다.
앞으로도 이러한 원리 기반 문제 풀이를 통해
단순 암기가 아닌 구조역학적 사고력을 기르는 데 도움을 드리겠습니다.
'재미있는 문제- 쉬운풀이 > 정정 보의 곡률, 처짐' 카테고리의 다른 글
| 2017년 서울시 7급 응용역학 1번 (순수휨 정정보의 처짐을 산정하는 여러방법) (0) | 2025.12.22 |
|---|---|
| 2007년 7급 국가직 응용역학 19번 (처짐을 빠르게 구하는 사고) (0) | 2025.11.30 |
| 2025년 7급 응용역학 가형 22번 풀이 (공액보법으로 푸는 방법) (0) | 2025.11.11 |
| 공액보법의 응용으로 쉽게 풀기 (2025년 서울시 7급 13번) (0) | 2025.11.07 |
| 2022년 9급 국가직 응용역학 개론 10번 - 보기를 통한 합리적 추론 기술 (0) | 2025.10.31 |