
1. 개요
이 문제는 전형적인 변위일치 문제로 접근할 수도 있습니다.
하지만 풀이의 초점을 변위 자체에 두느냐, 아니면 FEM - Fixed End Moment 을 활용하느냐에 따라 접근 방식이 달라집니다.
저는 이번 글에서 FEM을 이용하여 반력을 산정하고자 합니다.
중요한 것은 새로운 방법을 적용시 얼마나 통찰력 있게 다른 시각을 적용해 빠르게 풀 수 있는가, 그리고 다른 문제에도 확장성이 있는가입니다.
FEM 개념을 활용하는 것은 이러한 관점에서 보면 매우 만족스러운 풀이라고 할 수 있습니다.
2. 실전 풀이 (30초 컷)
FEM을 활용하면 다음 한줄의 풀이로 모든 것이 끝납니다.
$(\frac{-3EI}{L^2}\delta + \frac{wL^2}{8})\times\frac{1}{L}+\frac{w\times L}{2}=\frac{w\times L}{4}$
정리하면
$(\frac{3EI}{L^2}\delta - \frac{wL^2}{8})=\frac{w L^2}{4}$
따라서 답은
$\therefore \delta =\frac{wL^4}{8EI}$
3. 감각 잡기
위의 풀이에 대해 이해하기 쉽게 풀이하도록 하겠습니다. 문제도 B점에서 수직 반력이 $\frac{w L^2}{4}$ 만큼 생겼다면으로 변경할 수 있습니다
우선 위의 구조물은 B를 기준으로 대칭이므로 고정단으로 변경합니다.
위의 식이 나온 논리는 다음과 같습니다.
① $ \frac{-3EI}{L^2}$ x δ : δ만큼 처짐이 발생하였을 때 FEM
② $ \frac{wL^2}{8}$ : 하중 $w$ 에 의한 FEM
③ $ \times\frac{1}{L}$ : 모멘트 불균형에 의한 전단력
④ $ \frac{w\times L}{2}$ : 고정단 모멘트 효과를 제외하고 하중 $w$에 의한 반력
즉, 공식의 의미는 "FEM에 의한 전단력과 하중 $w$ 에 의한 반력을 더했더니 $\frac{w L^2}{4}$만큼 B에 반력이 생겼다" 라고 할 수 있습니다.
유도 과정을 그림으로 하면 다음과 같습니다.
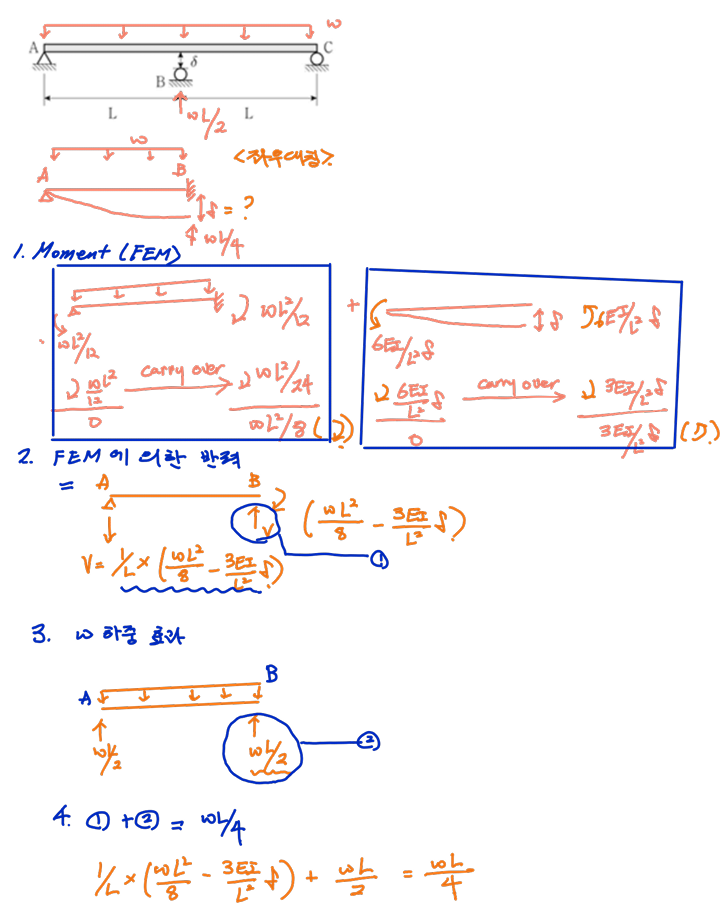
4. 정석 풀이 (변위일치 풀이)
4. 정리하며
결국 FEM 방식은 FEM에 대한 공식을 암기하고 있어야 하며 변위일치 방식은 재료역학 뒤 appendix 부분의 공식을 잘 암기하고 있어야 한다.
두개의 다른 접근, 그리고 두개의 다른 공식, 그리고 같은 답이 도출되었다.
결국 FEM 방식은 FEM 관련 공식을 반드시 암기하고 있어야 하고,
변위일치 방식은 재료역학 교재 뒤 Appendix에 실린 처짐 공식을 잘 기억하고 있어야 합니다.
즉, 서로 다른 접근 — 서로 다른 공식 — 그러나 도출되는 답은 동일합니다.
이 점이 바로 구조역학 문제 풀이의 묘미이며,
시험에서는 어떤 방식이든 자신에게 익숙한 방법으로 빠르게 답을 내는 것이 가장 중요합니다.
① FEM 방법
$$(\frac{-3EI}{L^2}\delta + \frac{wL^2}{8})\times\frac{1}{L}+\frac{w\times L}{2}=\frac{w\times L}{4}$$
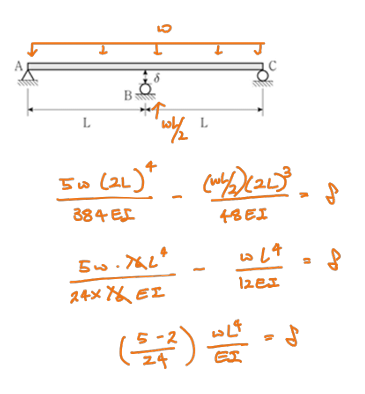
② 변위 일치법
$$\frac{5w\times(2L)^4}{384EI}-\frac{0.5wL\times(2L)^3}{48EI}=\delta $$
재료역학 교재 뒤 Appendix의 공식을 모두 암기하지 않았더라도,
FEM 방식을 활용하면 충분히 문제를 풀 수 있다는 사실을 꼭 기억해 두세요.
특히 FEM에 익숙해지면
- 등가하중 - Equivalent Nodal Force 개념이 자연스럽게 이해되고,
- Moment 분배법 같은 다른 해법을 적용할 때도 훨씬 수월해집니다.
즉, 공식 암기만으로는 얻기 힘든 구조 해석의 직관을 키울 수 있는 것이 FEM 접근법의 큰 장점입니다.