
1. 개요
이전 글에서는 지점 침하(Settlement) 를 변위법(특히 처짐각법) 으로 어떻게 해석하는지 자세히 설명드렸습니다.
https://oreostructure.tistory.com/58
보 구조물 변위법의 기본 - 처짐각법 pt 2
1. 개요이번 글은 처짐각법 Pt.1에 이어 두 번째 글입니다.https://oreostructure.com/48 보 구조물 변위법의 기본 - 처짐각법 pt 11. 개요단순보 양끝에 모멘트가 작용하면 휨은 어떻게 될까요?구조물을 스
oreostructure.com
핵심은, 지점 침하를 추가적인 변위가 아닌 “현 회전각(Chord Rotation)”으로 바라보는 관점입니다.
이 관점을 적용하면, 복잡해 보이는 문제라도 변위법을 통해
매우 간단하고 일관된 방식으로 해결할 수 있습니다.
일반적으로 부정정 차수가 클수록 변위법의 효율성은 더욱 커집니다.
이번 문제는 1차 부정정 구조물이며,
정정 구조물과 달리 지점에 침하가 발생하면
그 침하를 억제하려는 힘이 생기면서 부재력이 발생하게 됩니다.
특히 보 구조물에서는 이러한 외부 영향(침하, 온도, 제작 오차 등)에 대해
휨 모멘트(Bending Moment) 로 저항하게 되므로 정확한 처짐·회전·부재력 해석이 중요합니다.
이번 글에서는 이 문제를 처짐각법과 모멘트 분배법을 활용하여
어떻게 빠르고 효율적으로 풀 수 있는지 단계적으로 정리하여 설명드리겠습니다.
2. 문제 풀이
(1) 지점 침하에 따른 FEM 산정

FEM은 현회전각을 통해 다음과 같이 표현할 수 있습니다.

이를 그림에 표현해보면 다음과 같습니다.
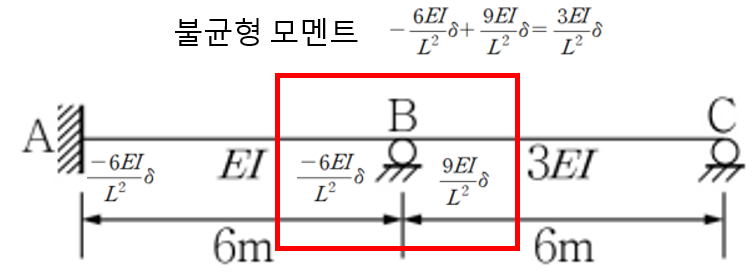
지점 B를 기준으로 휨에 대한 강성도를 살펴보면

이므로 강성도의 비율은 다음과 같습니다.

따라서 불균일 모멘트를 부재의 강성도 비율만큼 빼주면 됩니다.

따라서 답은

③번이 됩니다.
3. 마무리하며
얼핏 보면 다소 당황스러운 형태의 문제일 수 있습니다.
하지만 지점 침하(Settlement) 는 처짐각법(Slope-Deflection) 을 활용하면
간단하게 등가 부재력(불균형 모멘트) 으로 치환할 수 있으며,
이때 발생하는 불균형 모멘트(unbalanced moment) 는
모멘트 분배법(Moment Distribution Method) 으로 매우 쉽게 분배하여
각 부재력까지 자연스럽게 구할 수 있습니다.
서두에서도 말씀드렸듯이,
시험장에서 순간적으로 “어떤 전략을 써야 하나?” 하고 망설여진다면
우선 다음 원칙을 떠올리시면 됩니다.
- 부정정 차수가 있을수록 → 변위법(Slope-Deflection, Virtual Work)을 우선 고려한다.
- 보(Beam) 구조물일 경우 → 모멘트를 중심으로 판단하고 푸는 것이 가장 빠르다.
즉, 지점 침하·온도·제작오차처럼 외부 요인이 있는 문제일수록
변위법 기반 접근이 훨씬 명확하고 안정적으로 해결됩니다.
'재미있는 문제- 쉬운풀이 > 부정정 보의 해석' 카테고리의 다른 글
| 2026년 7급 근로감독 산업안전 응용역학 23번 (변위법적인 쉬운 접근) (0) | 2026.01.26 |
|---|---|
| 2019년 7급 국가직 응용역학 10번 (부정정 보 처짐의 쉬운 풀이) (0) | 2026.01.20 |
| 2009년 7급 국가직 응용역학 5번 문제 (변위 기반의 생각) (0) | 2025.12.06 |
| 2015년 7급 서울시 응용역학 10번 (해답을 넘은 해설 : 영향선과 FEM) (0) | 2025.11.26 |
| 가상 변위의 법칙으로 강성도 산정 및 등가하중으로 처짐 구하기 (2024년 서울시 7급 16번) (0) | 2025.11.03 |