
1. 개요
이번 문항은 케이블의 일반 정리(General Cable Theorem) 를 활용하면 매우 빠르고 간단하게 해결할 수 있는 문제입니다.
이번 포스팅에서는
- 먼저 케이블의 일반정리를 이용한 가장 효율적인 풀이를 보여드리고,
- 이어서 해당 문항에서 필요한 일반정리를 직접 유도해 본 뒤,
- 마지막으로 일반정리를 사용하지 않고 푸는 방법도 가능한지 비교해 보도록 하겠습니다.
케이블 문제는 처음 보면 복잡해 보이지만, 핵심만 잡고 나면 훨씬 단순해집니다.
특히 시험장에서는 “일반정리 활용 → 순간 해결”이 가장 큰 이점이 됩니다.
2. 케이블의 일반정리를 활용한 문제 풀이
집중하중 PP가 작용하는 케이블에서,
해당 하중점의 현(chord)—즉, 케이블 양 끝을 직선으로 이은 선—까지의 수직거리를 ym 이라고 하면,
케이블의 수평분력 H는 다음 관계를 만족합니다.

H×ym= 등가 단순보의 모멘트
즉, 케이블 문제를 단순보의 모멘트 문제로 변환하는 것이 바로 ‘케이블의 일반정리’입니다.
이 정리를 활용하면 굳이 복잡한 처짐방정식이나 장력 분해를 거치지 않아도 되므로,
7급·9급 시험에서는 사실상 가장 빠르고 안전한 풀이법이라고 할 수 있습니다.
케이블의 일반정리를 위의 문항에 적용해 보겠습니다.

손쉽게 수평력(H)= 60 kN로 산정 됩니다.
3. 케이블 일반정리 유도
지점 A에서 x 만큼 떨어진 곳을 m 이라 하고 케이블 구조와 등가 단순보를 나란히 놓겠습니다.
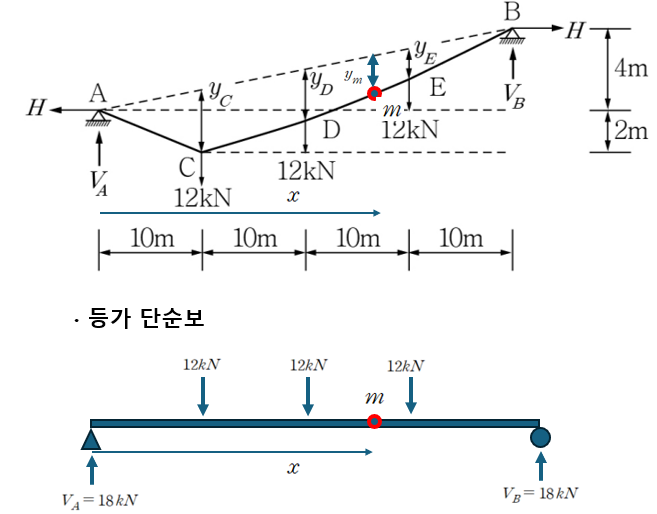
케이블에서 수직 반력을 산정해 보면 다음과 같습니다.

이때 m 지점에서의 모멘트 식을 세우고 해당 값이 0이라는 식을 세우면 다음과 같습니다.

해당 식에 위에서 구한 VA를 대입하면 다음과 같습니다
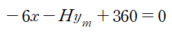
한편 등가 단순보에서 모멘트를 구하면 다음과 같이 표현할 수 있습니다.
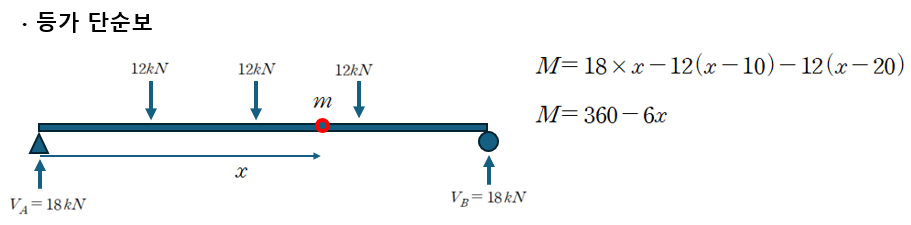
케이블에서 산정한 식과 비교하여 대입해 보면 다음과 같습니다.
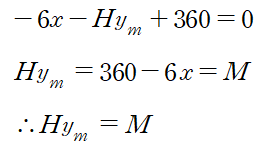
이로서 개요에서 언급한 케이블 일반 정리를 유도하였습니다.
4. 케이블 일반정리 활용하지 않는 풀이
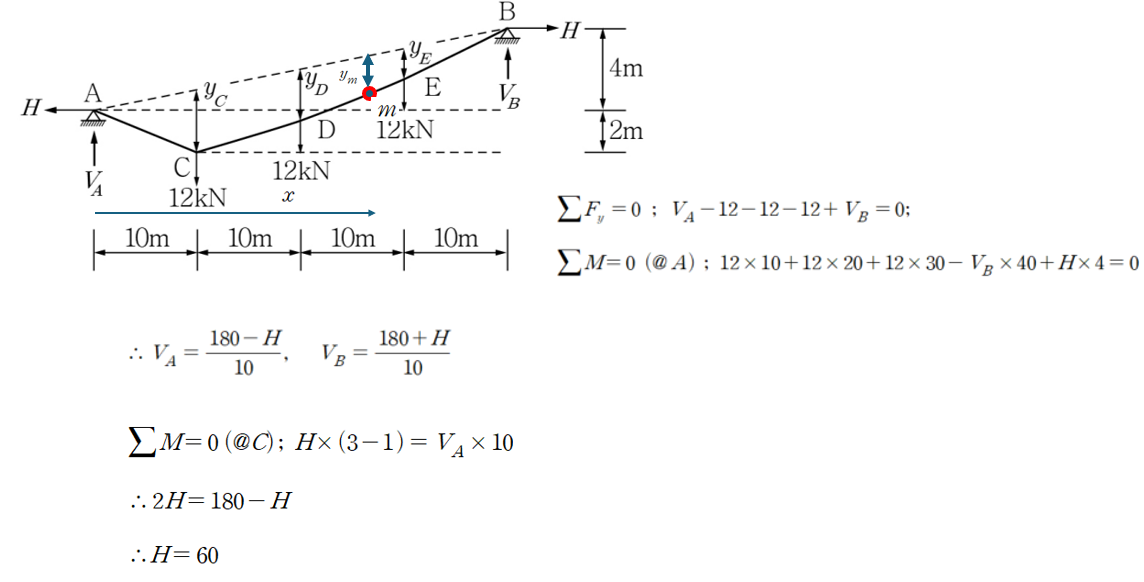
케이블의 모든 부분의 모멘트는 0이다라는 조건을 활용하여 풀면 케이블의 일반정리를 사용하지 않고 문제를 풀 수 있습니다.
케이블은 모멘트에 저항하지 못하고 인장력으로서 축력에 저항할 수 있기 때문입니다.
5. 마무리 하며
케이블은 모멘트에 저항할 수 없는 하중전달체이기 때문에, 내부모멘트가 항상 0이 되는 조건을 잘 활용하면 일반정리를 사용하지 않고도 문제를 풀 수 있습니다. 이론적으로는 분명 가능합니다.
하지만 실제 시험장 상황을 가정해 보면, 일반정리를 사용하지 않는 접근은 여러모로 비효율적입니다.
우선 케이블 문제를 직접 해석하려면
- 케이블의 수평력 H 을 미지수로 두고 반력을 구해야 하고
- 그 반력을 다시 하중점의 모멘트 평형식에 대입해야 합니다.
이 과정은 연산이 길어지고, 항이 많아지며, 중간에서 실수가 발생할 가능성도 높습니다.
특히 7급·9급처럼 손계산 중심의 시험에서는 큰 부담일 수 있습니다.
따라서 케이블의 일반정리는 단순한 편의공식이 아니라,
시간·정확도·연산 효율을 모두 확보하기 위한 실전 전략이라고 보시는 것이 좋습니다.
이번 포스팅에서는
- 케이블 일반정리가 왜 성립하는지 유도 과정을 보여드렸고
- 이 정리를 일부러 사용하지 않고 풀 수 있는 방식도 소개해드렸습니다.
(이것은 개념 이해용으로는 매우 좋습니다.)
그러나 실전 풀이에서는 고민 없이 일반정리를 활용하시길 권해드립니다.
시험장에서 짧은 시간 내에 실수 없이 정답에 도달하기 위해서는
케이블의 일반정리가 가장 강력한 도구이기 때문입니다.