안녕하세요. 오레오 구조입니다.
이번 포스팅에서는 필수적으로 알아두어야 할 FEM(Fixed End Moment) 공식 몇 가지를 직접 유도해 보고,
이를 실제 문제풀이에 어떻게 활용할 수 있는지까지 함께 다뤄보려고 합니다.
제 블로그를 꾸준히 보신 분들은 아시겠지만,
저는 반력이나 처짐을 구할 때 FEM과 이를 기반으로 한 등가절점하중 개념을 매우 자주 활용합니다.
그만큼 계산을 줄이고, 구조물의 거동을 직관적으로 파악하는 데 효과적인 도구이기 때문입니다.
다만 메일이나 댓글을 통해 종종 이런 질문을 받습니다.
- FEM은 어디까지 암기해야 하나요?
- 공식이 많은데, 전부 외워야 하나요?
- FEM 공식은 어떤 가정에서 어떻게 유도되는 건가요?
이처럼 FEM을 단순 암기 대상으로 받아들이면서 혼란을 느끼시는 분들이 있는 것 같아,
이번 글에서는 공식을 나열하기보다는, 꼭 필요한 FEM만 선별하여 그 유도 과정을 차근차근 살펴보는 것을 목표로 합니다.
공식이 왜 그렇게 생겼는지를 이해하고 나면
암기 부담은 자연스럽게 줄어들고,
등가절점하중이나 모멘트 분배법, 변위일치 문제에서도 훨씬 자유롭게 활용할 수 있게 됩니다.
FEM을
‘외워야 할 공식’이 아니라
‘필요할 때 스스로 만들어 쓸 수 있는 도구’로 바꾸는 것이
이번 포스팅의 핵심입니다.
차근차근 같이 정리해 보겠습니다.
참고로 다양한 방법으로 유도를 해보겠습니다. 비교적 간편하고 효율적인 손계산 연산법을 제시 하겠습니다.
그러니 암기하시면서 따라해보시기 바랍니다. 이를통해 다양한 계산의 tool을 익히게 되는 기회가 되시면 좋겠습니다.
Case 1 : 집중하중이 작용하는 보부재의 FEM

1. 변위 일치 방법 (공액보법)
① 공액보법을 활용한 단순보에서의 회전각 산정
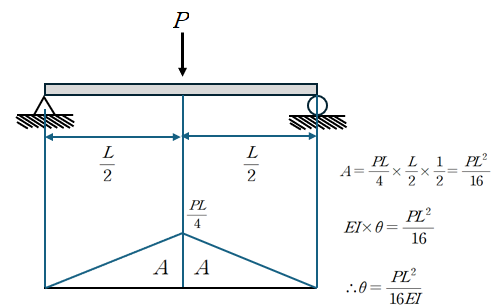
② 회전각을 0으로 만드는 양단 고정단 모멘트 산정
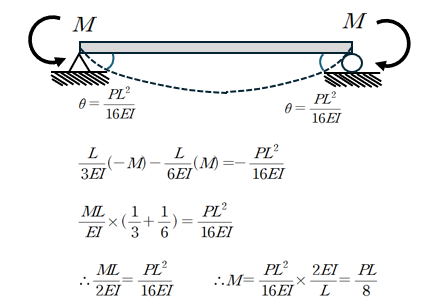
2. 처짐각법 방법
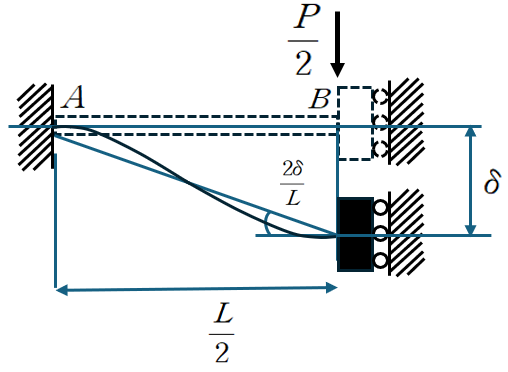
대칭을 활용하여 Fixed Roller로 모델링 후, 시계방향을 양의 값으로 가정하면
다음과 같은 부재력과 변위간 관계식을 세울 수 있습니다.
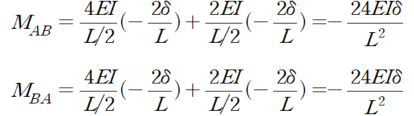
가상 변위의 법칙을 세우게 되면

중앙 값의 처짐은 다음과 같이 산정 할 수 있습니다.
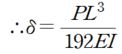
이를 위의 부재력 변위간 관계식에 대입하게 되면

Case 2 : 등분포하중이 작용하는 보부재의 FEM
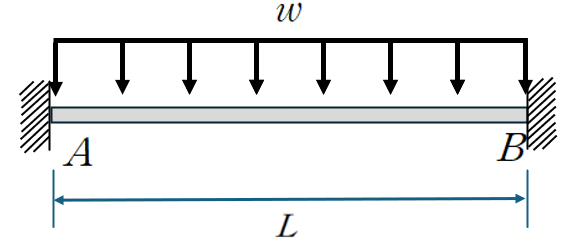
1. 변위 일치 방법 (공액보법)
① 공액보법을 활용한 단순보에서의 회전각 산정

** 참고 [모멘트 면적법의 방식으로도 산정 가능]
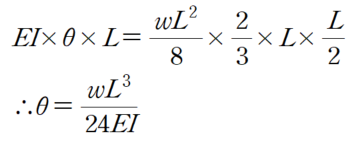
② 회전각을 0으로 만드는 양단 고정단 모멘트 산정

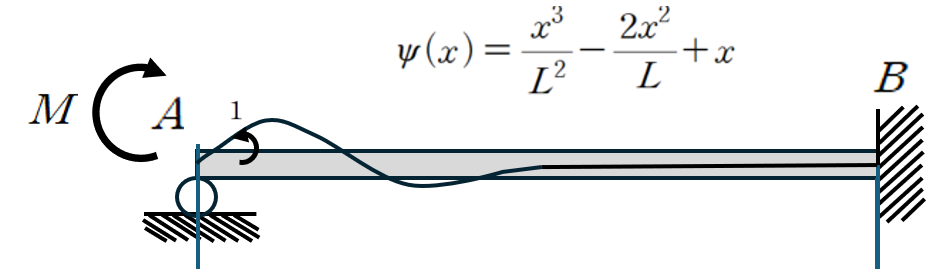
2. 형상 함수 이용한 가상 변위의 법칙
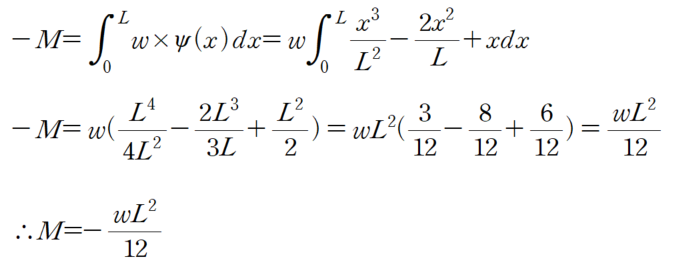
'응용역학-구조역학 필수 이론' 카테고리의 다른 글
| FEM 공식 유도 및 응용 (Ⅲ) (1) | 2026.01.20 |
|---|---|
| FEM 공식 유도 및 응용 (Ⅱ) (1) | 2026.01.19 |
| 비틀림에 대한 이론 Ⅰ (원형 단면적을 갖고 있는 Shaft) (0) | 2026.01.12 |
| 수정된 처짐각 법 - 처짐각 법 pt 4 (연산을 가볍게) (0) | 2025.12.02 |
| 보 구조물 변위법의 기본 - 처짐각법 pt 3 (FEM 과 등가 절점 하중) (4) | 2025.11.12 |