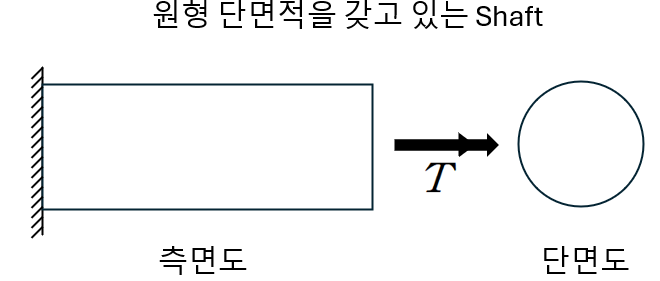
1.개요
일반적으로 많은 분들이 비틀림 문제를 공식 암기와 단순 대입 방식으로 접근합니다.
선형 탄성 범위 내에서 출제되는 전형적인 문제라면 이러한 접근으로도 충분히 해결이 가능합니다.
하지만 문제가 조금만 변형되어 단면 내부에 소성변형 구간이 존재하거나, 기존의 선형 탄성 가정을 벗어나는 조건이 주어지면 많은 수험생들이 갑자기 문제 접근 자체를 어려워하는 모습을 보게 됩니다.
이는 비틀림을 하나의 “공식 문제 유형”으로만 인식하고, 그 공식이 어떤 가정과 원리에서 유도되었는지를 충분히 이해하지 못한 데서 오는 한계라고 생각합니다.
비틀림 문제가 기존에 알고 있던 선형 탄성 영역을 벗어나거나, 응력 분포가 달라지는 상황으로 확장될 때에는 단순 암기한 공식이 더 이상 유효하지 않을 수 있습니다.
이럴 때 우리는 다시 출발점으로 돌아가, 비틀림(Torsion)이 주어진 원형 샤프트에서 어떤 기하학적 변형 과정을 거쳐 유도되었는지를 떠올릴 필요가 있습니다.
즉, 비틀림에 대한 근본적인 기하학적 해석과 변형의 의미를 이해하고 있다면, 소성 비틀림이나 비선형 거동을 다루는 문제에서도 훨씬 수월하게 접근할 수 있습니다.
이러한 이유로 본 포스팅에서는 비틀림 공식을 바로 적용하기에 앞서, 비틀림의 기하학적 원리와 기본 가정이 무엇인지부터 차근차근 정리해보고자 합니다.
2. 핵심 기하학 (Ⅰ)

우선 위 그림과 같이 비틀림 (Torsion)을 받고 있는 반지름 R의 단면적에서 임의의 길이 ρ 만큼 떼어내어 아래와 같이 기하학적 관계를 따져보겠습니다.

비틀림에 의한 전단변형률 γ 은 각도로서 정의 됩니다. 미소변형의 가정하에 Shaft 끝부분 에서 BB' 의 길이는 L×γ 로 표현될 수 있습니다. 이는 기하학적으로 단면내 비틀림 각도 (θ)와 임의의 길이인 ρ 를 곱한 것과 일치하게 됩니다.
이로서 우리는 비틀림에 의한 전단 변형률을 산정할 수 있습니다.
2. 핵심 기하학 (Ⅱ)

우리는 단면내 거리 ρ 만큼 떨어진 미소요소 dA가 전단응력 τ 을 갖고 있을 때 이에 대한 미소 Torque를 산정할 수 있으며
이를 전단면적에 걸쳐 적분 할 경우 Torque가 산정 됩니다.
3. 전단응력 - 전단변형률 관계 대입
전단응력은 아래와 같이 표현할 수 있습니다.

이를 위에서 산정한 Torque 공식에 대입하게 되면

즉, Torque는 다음과 같이 정리할 수 있습니다.
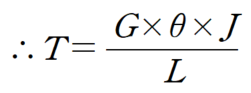
4.비틀림 공식의 정리
지금까지 유도한 공식들을 한곳에 모아 정리하면 다음과 같이 표현 할 수 있습니다.

따로따로 공식을 암기하시는 것 보다 위의 공식을 암기하고 주어진 조건에 맞게 활용하시면 좋습니다.
5. 비틀림에서의 응력상태 (응용되어 출제에 활용)
비틀림에서의 응력은 순수 전단응력 상태입니다.
이를 요소와 모아원(Mohr's Circle)으로 그리면 아래의 그림과 같습니다.

만약 인장응력에 취약한 취성물질 (Brittle Material)이면 모아원 (Mohr's Circle) 에서 볼 수 있듯이 45˚ 각도에서 취성파괴가 일어나게 됩니다. 그리고 이때의 항복강도 σy는 전단응력인 τxy와 동일하게 됩니다.
이와 같은 성질을 활용한 문제가 2021년 지방직 7급 응용역학 8번에 출제된 바 있습니다.
https://oreostructure.tistory.com/105
2021년 지방직 7급 응용역학 풀이 (필요한 것만 빠르게 취하는 풀이)
“바로 풀린다” 리스트 (문제당 30초 내외)1 (휨응력-환산단면의 전형적인 유형), 2 (기본 조합하중), 3 (단면 2차 모멘트와 단면계수의 기본), 4 (전단 변형률의 기본), 5 (소성모멘트의 전형적인 유
oreostructure.com
6. 탄소성 비틀림 (응용되어 출제에 활용)
2022년 지방직 응용역학 10번에 출제된 바 있습니다.
https://oreostructure.tistory.com/114
2022년 지방직 7급 응용역학 풀이 (전략이 있는 풀이의 필요성)
바로 풀린다” 리스트 (문제당 30초 내외)1 (단면계수의 특성), 2 (모아원의 기본 특성), 3 (탄성계수와 강도 기본 개념), 4 (정정보에서의 영향선- 뮐러 브레스라우), 5 (단면2차모멘트의 특징)7 (소성
oreostructure.com
탄소성이라 해서 거부감을 느끼실 필요 없습니다.
탄성에서 활용하였던 본 포스팅의 핵심기하학 Ⅱ 을 활용해보시면 됩니다.
여기서 dA는 그림에서 볼 수 있듯 ρ×dθ×dρ 가 됩니다.
문제와 풀이는 위 링크를 활용하시면 됩니다.
극좌표계에 거부감을 느끼지 마시고 쉽게 푸시면 좋습니다.
7. 비틀림 부정정해석 (응용되어 출제에 활용)
아래와 같이 양단고정의 길이 L인 원형 Shaft에 길이 a만큼 떨어진 지점에서 비틀림 Torsion이 작용한다고 했을때
번력 TA와 TB를 산정한다고 하면 변위일치로 다가갈 수 있습니다.
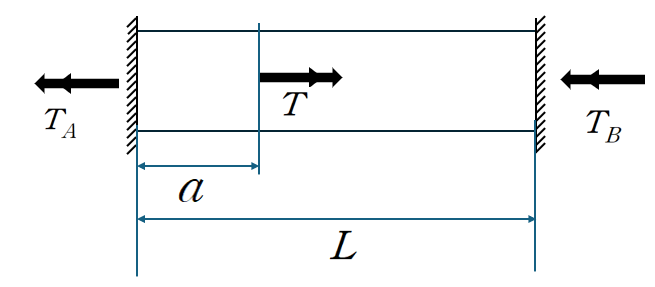
B지점을 자유단으로 하였을때 Shaft의 비틀림각을 산정하겠습니다.
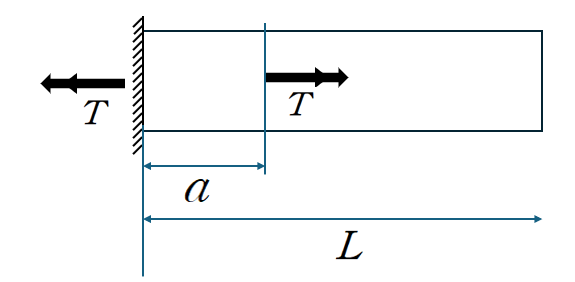
이때 자유단의 비틀림각은 공식에 의해 다음과 같이 산정됩니다.
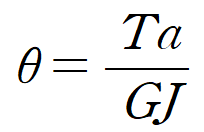
이제 TB를 가하여 해당 비틀림각을 0으로 만들도록 하겠습니다.

따라서 적합방정식에 따라

가 성립하게 됩니다.
따라서 TA는 힘의 평형에 의해

따라서 부정정 비틀림 문제를 풀때 부정정 축부재와 성격이 매우 비슷함을 알 수 있습니다.
2025년 서울시 7급 1번문제를 이와 같은 원리를 활용하여 쉽게 풀 수 있습니다.
https://oreostructure.tistory.com/51
2025년 7급 서울시 응용역학 풀이 (유연도와 강성도에 익숙해지자)
“바로 풀린다” 리스트 (문제당 30초 내외)1, 2, 3, 6 (부재의 부피 산정 매우 간단), 7(보기 활용), 9 (출제자의 배려), 10 (보기 활용)11 (변위일치 공식을 알려줌), 13(전형적인 유형), 14 (가상일의 원
oreostructure.com
'응용역학-구조역학 필수 이론' 카테고리의 다른 글
| FEM 공식 유도 및 응용 (Ⅱ) (1) | 2026.01.19 |
|---|---|
| FEM 공식 유도 및 응용 (Ⅰ) (2) | 2026.01.18 |
| 수정된 처짐각 법 - 처짐각 법 pt 4 (연산을 가볍게) (0) | 2025.12.02 |
| 보 구조물 변위법의 기본 - 처짐각법 pt 3 (FEM 과 등가 절점 하중) (4) | 2025.11.12 |
| 보 구조물 변위법의 기본 - 처짐각법 pt 2 (7) | 2025.11.10 |