1. 개요
이번 글은 처짐각법 Pt.1에 이어 두 번째 글입니다.
보 구조물 변위법의 기본 - 처짐각법 pt 1
1. 개요단순보 양끝에 모멘트가 작용하면 휨은 어떻게 될까요?구조물을 스프링처럼 단순 모델로 치환하는 직관은 유용하지만, 보는 단자유도 스프링과 달리 양단 회전이 독립적으로 존재합니다
oreostructure.com
이번에는 보의 한 지점에서 지점 침하(Settlement) 가 발생했을 때
이를 어떻게 해석해야 하는가에 대해 다뤄보겠습니다.
이때 핵심은 두 가지입니다.
첫째, 지점 침하로 인해 양단 모멘트가 어떻게 발생하는지,
둘째, 이 모멘트가 보의 회전량과 어떤 관계를 가지는지를 이해하는 것입니다.
이번 포스팅에서는 이러한 과정을 순수한 기하학적 변형도(Deformation Diagram) 를 바탕으로
하나씩 분석해 나가겠습니다.
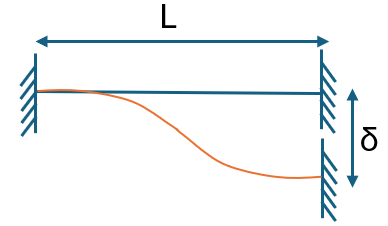
그림과 같이 고정단–고정단 조건(Fixed–Fixed Beam) 으로 설정한 이유는,
지점 침하의 효과만을 순수하게 살펴보기 위해
양단의 회전을 완전히 구속한 상태로 두기 위함입니다.
양단 절점을 각각 A와 B로 두었을 때,
지점 침하로 인해 내부 모멘트와 전단력(Shear) 이 새롭게 발생하게 됩니다.
이에 따라 아래 그림과 같이 침하 후의 변형 상태와 내부력 분포를 함께 표시하여
해석을 진행하도록 하겠습니다.

2. 이중적분 방법을 통한 기하학적 해석
(1) Free Body Diagram
임의의 x 만큼 떨어진 곳에서의 Free Body Diagram은 다음과 같습니다. 또한 좌표축 설정도 그림과 같이 표기해두었습니다.

(2) 곡률을 활용한 이중 적분
이제 아래의 기본식을 이용하여 처짐곡선 y를 구해보도록 하겠습니다.
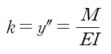
이때 모멘트 Ma 와 전단력 Va 는 아직 구해지지 않은 미지수 상태로 두고,
경계조건(Boundary Condition) 을 적용하여 단계적으로 풀어나가겠습니다.

이때 A지점 (고정단) 에서 경계조건을 적용시,

또한 B지점 (고정단) 에서 경계조건을 적용시,
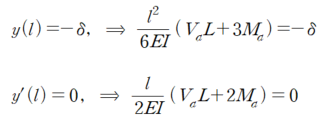
이에 대한 연립방정식을 풀면 모멘트 Ma 와 전단력 Va 는 다음과 같이 산정 됩니다.

(3) δ 만큼 지점 처짐에 대한 절점 하중
위에서 산정한 결과를 바탕으로 반대편 절점의 하중을 힘의 평형으로 구해보면 다음과 같습니다.

즉, δ 만큼 지점 침하가 발생하였을때, 아래와 같이 정리할 수 있습니다.

3. 지점침하의 각도 치환
사실 6EI/L^2 이라는 것은 다음과 같이 쓸 수 있습니다.
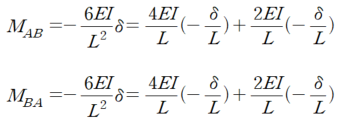
즉, δ 만큼의 처짐을 현회전각 (δ/L)로 치환하여 쓸수 있습니다.
현회전각의 기하학적 표현은 다음 그림과 같이 나타낼 수 있습니다.
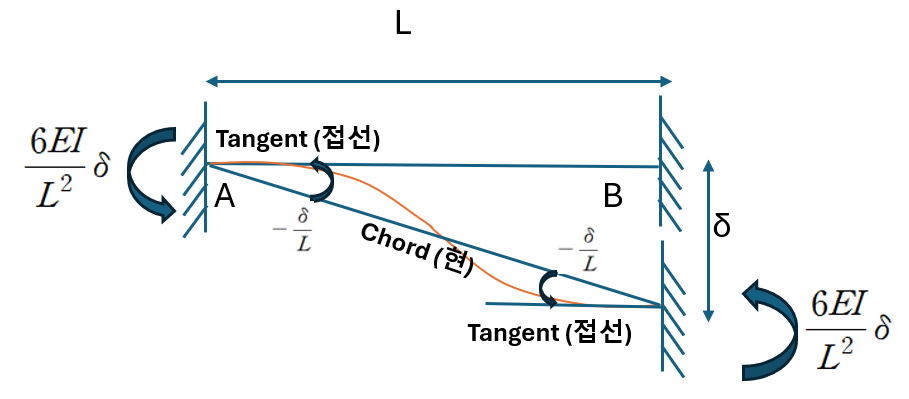
즉, 현 회전각(Chord Rotation Angle) 은
각 절점을 일직선으로 연결한 현(Chord) 과,
그 지점에서의 처짐곡선의 접선(Tangent) 사이의 각도로 표현할 수 있습니다.
처짐각법에서는 일반적으로 시계방향 회전을 양(+)의 값으로 정의합니다.
따라서 그림에서 보듯이,
지점 침하로 인해 부재가 시계방향으로 회전하게 되면,
이에 대응하는 현 회전각은 반시계방향, 즉 음(-)의 값으로 발생하게 됩니다.
4. 마무리하며
이제부터 지점침하를 하나의 또다른 변수로 생각하지 않아도 됩니다.
현회전각으로 포함시켜 다음과 같이 표현 할 수 있습니다. 이제부터는 지점 침하(Settlement) 를 별도의 변수로 취급하지 않아도 됩니다.
침하에 의한 효과를 현 회전각(Chord Rotation) 으로 포함시켜
다음과 같이 표현할 수 있습니다.

보가 선형탄성체(Linear Elastic Body) 라는 점을 고려하면,
중첩의 원리(Superposition Principle) 가 그대로 적용됩니다.
따라서 지점 침하 또한 회전각의 형태로 포함시켜,
보 구조물을 양단 회전만 존재하는 2자유도 부재(two-degree-of-freedom member) 로
단순화하여 해석할 수 있습니다.
'응용역학-구조역학 필수 이론' 카테고리의 다른 글
| 수정된 처짐각 법 - 처짐각 법 pt 4 (연산을 가볍게) (0) | 2025.12.02 |
|---|---|
| 보 구조물 변위법의 기본 - 처짐각법 pt 3 (FEM 과 등가 절점 하중) (4) | 2025.11.12 |
| 보의 처짐 - 이중적분과 공액보법 (0) | 2025.11.05 |
| 자유진동 Free Vibration 과 고유진동수 (0) | 2025.11.04 |
| 보 구조물 변위법의 기본 - 처짐각법 pt 1 (0) | 2025.10.30 |