반응형
1. 스프링의 직렬 연결

① 구조적 의미
두 개 이상의 스프링이 한 줄로 연결되어 한 점에서 다음 점으로 순차적으로 하중을 전달하는 형태입니다.
즉, 모든 스프링에 걸리는 힘은 동일하지만, 변형(변위)은 각 스프링마다 독립적으로 발생합니다.
스프링을 여러 개 줄줄이 이어 붙인 모습을 떠올려보세요.
마치 침대 매트리스의 스프링을 세로로 한 줄로 쌓아 놓은 모양입니다.
이런 상태에서 위에서 누르면,
수직 배열된 스프링에 같은 힘이 전달되지만,
각 수직 배열된 스프링이 눌리는 정도(변형) 는 다를 수 있습니다.
② 자유도 관점
- 각 스프링은 자체적으로 늘어나거나 줄어들 수 있으므로,
구조 전체의 자유도는 스프링 수에 따라 증가합니다. - 예를 들어, 위 그림처럼 고정점–스프링1–스프링2–하중점 형태라면,
스프링1과 스프링2의 변형은 독립적이므로 2개의 내부 자유도가 존재합니다. - 단, 하중점의 전체 변위는 두 스프링의 합으로 표현되므로, 외부적으론 1개의 전체 변위 자유도로 보이지만, 내부적으로는 2개의 독립된 변형 자유도를 가집니다. (즉, 각 스프링이 눌리는 정도, 변형은 다를 수 있습니다)
③ 등가 강성도 (Keq)

2. 스프링의 병렬 연결
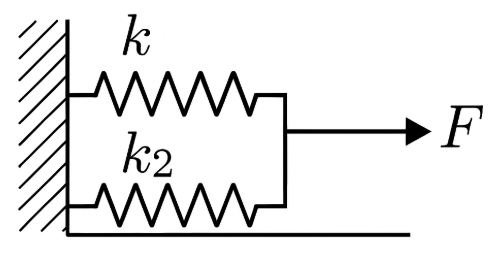
① 구조적 의미
두 개 이상의 스프링이 같은 두 점을 동시에 연결하여 하중을 분담하는 형태입니다.
즉, 각 스프링의 변위는 동일하지만, 하중은 각 스프링이 나누어 받습니다.
② 자유도 관점
- 모든 스프링이 같은 두 점 사이에 연결되어 있으므로,
독립적인 변형 자유도는 1개뿐입니다. - 즉, 전체 구조의 거동은 단일 자유도 시스템처럼 작동합니다.
(모든 스프링이 같은 변위를 공유하므로 내부 독립변형 없음)
③ 물리적 해석
- 변형이 같고, 하중이 분담되므로 전체 강성은 커집니다.
- 즉, 자유도가 적을수록 구조는 단단해짐(강성 증가).
④ 등가 강성

반응형
'응용역학-구조역학 필수 이론' 카테고리의 다른 글
| 자유진동 Free Vibration 과 고유진동수 (0) | 2025.11.04 |
|---|---|
| 보 구조물 변위법의 기본 - 처짐각법 pt 1 (0) | 2025.10.30 |
| EA가 무한할 때의 자유도와 종속 자유도 (0) | 2025.10.15 |
| 구조물의 자유도 (Degree of Freedom, DOF) (0) | 2025.10.15 |
| 강체 기둥 좌굴 - 반드시 빠르게 정답을 정확하게 도출하자 (3) | 2025.10.13 |