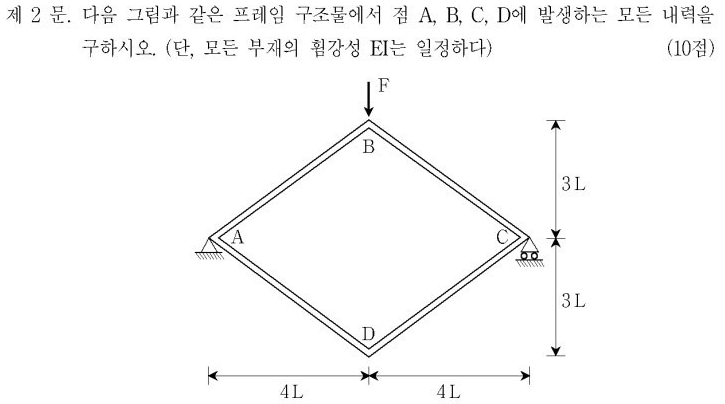
1. 풀이의 방향
요즘 구조기술사나 기술고시 문제 풀이를 보면, 공학용 계산기를 통해 최소일(에너지법) 혹은 매트릭스 변위법에만 의존하는 방식이 많다. 일부 강사는 “시험장에서 답만 맞추면 된다”는 논리로 최소일법이나 매트릭스 계산을 강조하지만, 이는 계산 중심의 훈련일 뿐 개념적 이해를 깊게 하지 못하는 방식이라 생각한다.
위 문제에 처짐각법으로 구성방정식을 세우고 이를 자연스럽게 매트릭스 형태로 확장하는 과정을 통해, 사람들이 흔히 별개의 방법이라 생각하는 두 접근이 사실상 같은 원리를 공유함을 보여주고자 한다.
2. 구조물 개요
이 구조물의 Global 자유도(DOF) 는 A, B, C, D 절점의 회전-Rotation 자유도 4개와 전체 구조물의 수평 혹은 수직 이동-Sway 자유도 1개를 포함하여, 총 5개의 자유도를 가진다.
자유도는 각 절점이 수학적으로 이동할 수 있는 가능성을 통해 쉽게 판단할 수 있다. 일반적으로 하나의 절점은 수평, 수직, 회전의 3가지 자유도를 가진다. 그러나 이 구조물의 경우,
- 절점 A의 수직 및 수평 자유도가 구속되어 있고,
- 절점 B의 수직 자유도가 구속되어 있다.
또한 프레임 구조물은 주로 휨 강성-bending stiffness 으로 변형에 저항하므로, 부재의 축방향 변위-axial deformation 는 일반적으로 무시한다. 이때 축방향 변형이 구속되는 부재의 개수가 4개이므로, 전체 자유도는 다음과 같이 계산된다.

따라서 이 구조물의 전체 자유도는 5개가 된다.
3. Kinematic 관계 및 대칭 modeling
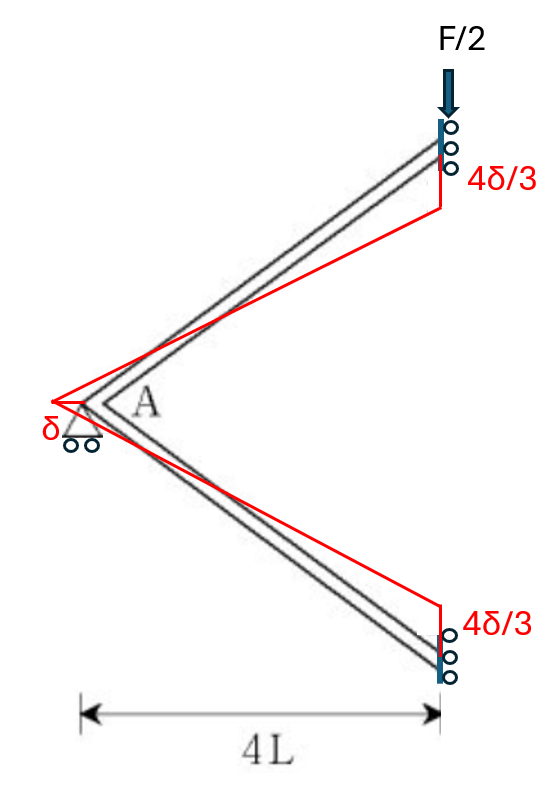
① 해당 구조물은 대칭이다. 따라서 절점 B와 D를 Fixed roller로 모델링 할 수 있다.
이때 하중도 F에서 F/2로 변경한다.
이 하중이 한 외부 가상일은 $\frac{4 \delta}{3}\times\frac{F}{2}$ 가 된다.
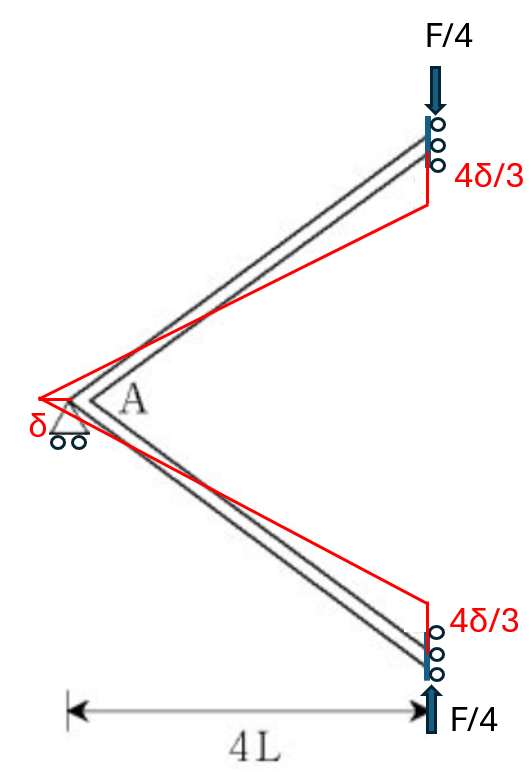
② 외부 가상일 $\frac{4 \delta}{3}\times\frac{F}{2}$ 는 2개로 나누어 서술할 수 있다.
$$\frac{4 \delta}{3}\times\frac{F}{2}=\frac{4 \delta}{3}\times\frac{F}{4} + \frac{4 \delta}{3}\times\frac{F}{2}$$
즉 절점 B와 D에서 각각 F/4의 하중이 각각의 변위인 4δ/3 만큼 가상의 일을 한다고 치환할 수 있다. 외부 가상일의 양은 그래도 변함이 없다.
③ 따라서 절점 A를 지나는 대칭축을 따라 다음과 같이 모델링이 가능하다.
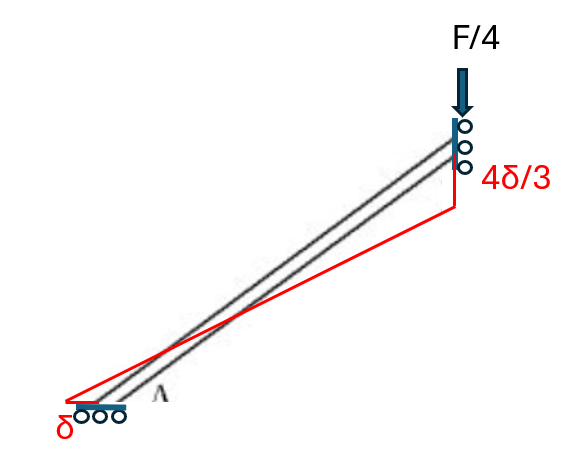
4. 구성 방정식
Kinematic 관계를 통해 얻은 부재 AB의 현회전각은 다음과 같다.
$$\frac{δ}{3L}$$
현회전각이 시계방향이므로 부재 內 각도는 chord에서 tangent로 정의되므로 이와 반대인 반시계방향이다.
여기서 시계방향 rotation을 +로 설정하여 풀이하겠다.
$$M_{AB}=\frac{4EI}{5L}\times\frac{-\delta}{3L}+\frac{2EI}{5L}\times\frac{-\delta}{3L}$$
$$M_{BA}=\frac{2EI}{5L}\times\frac{-\delta}{3L}+\frac{4EI}{5L}\times\frac{-\delta}{3L}$$
이를 매트릭스로 표현하면 다음과 같다.
$$\begin{bmatrix}M_{AB} \\M_{BA} \end{bmatrix}=\begin{bmatrix}\frac{4EI}{5L} & \frac{2EI}{5L} \\\frac{2EI}{5L} & \frac{4EI}{5L} \end{bmatrix}\times\begin{bmatrix}\frac{-1}{3L} \\\frac{-1}{3L} \end{bmatrix}\times\begin{bmatrix}\delta \end{bmatrix}$$
5. 가상 변위의 법칙
① 외부일은 $\frac{F}{4}\times \frac{4\delta}{3}$ 이다.
② 내부일은 $\frac{-M_{AB} \delta}{3L}-\frac{M_{BA} \delta}{3L}$ 이다.
$\delta$를 양변 소거 후 이를 매트릭스로 표현하면 다음과 같다.
$\begin{bmatrix}\frac{F}{4}\times \frac{4}{3} \end{bmatrix}=\begin{bmatrix}\frac{-1}{3L} &\frac{-1}{3L} \end{bmatrix}\times\begin{bmatrix}M_{AB} \\M_{BA} \end{bmatrix}$
6. 매트릭스 표현
가상변위의 법칙으로 산정한 식에 구성 방정식을 대입하면 다음과 같이 식이 완성된다.
$$\begin{bmatrix}\frac{F}{4}\times \frac{4}{3} \end{bmatrix}=\begin{bmatrix}\frac{-1}{3L} &\frac{-1}{3L} \end{bmatrix}\times\begin{bmatrix}\frac{4EI}{5L} & \frac{2EI}{5L} \\\frac{2EI}{5L} & \frac{4EI}{5L} \end{bmatrix}\times\begin{bmatrix}\frac{-1}{3L} \\\frac{-1}{3L} \end{bmatrix}\times\begin{bmatrix}\delta \end{bmatrix}$$
7. 답안 및 의의
부재력은 $\frac{-FL}{2}$가 나오며 양단 절점 모멘트와 이에 따른 Shear Force를 그려주면 된다. Axial Force는 축방향 강체로 가정하였으므로 고려하지 않는다.
이 포스팅의 목적은 단순히 정답을 제시하는 것이 아니다.
어떤 사람은 힘의 평형방정식을 통해 A 매트릭스를 구성하고,
또 어떤 사람은 운동학적 - Kinematic 관계를 이용해 B 매트릭스를 도출한다.
결국 두 방법은 본질적으로 동일한 접근이다.
다만 A 매트릭스 방식만 익숙한 사람은 대개 종속변위나 가상변위의 법칙에 대한 이해가 부족해, 어느 절점의 자유도를 선택하느냐에 매우 민감하다. 물론 이런 방식으로도 충분히 익숙해져서, 나름의 ‘공식’이나 ‘요령’을 터득하는 사람도 있다.
반대로 B 매트릭스를 사용하는 사람은 처음에는 운동학적 관계를 세우는 과정이 낯설고 복잡하게 느껴질 수 있다. 그러나 연습을 거듭하면 일정한 규칙성과 직관을 발견하게 되어 큰 어려움을 느끼지 않는다. 다만 이 역시 가상변위의 법칙에서 유도되는 관계의 의미를 이해하지 못한다면, 깊이 있는 접근이라고 보기는 어렵다.
'응용역학-구조역학 필수 이론' 카테고리의 다른 글
| 스프링의 직렬 연결과 병렬 연결 (2) | 2025.10.26 |
|---|---|
| EA가 무한할 때의 자유도와 종속 자유도 (0) | 2025.10.15 |
| 구조물의 자유도 (Degree of Freedom, DOF) (0) | 2025.10.15 |
| 강체 기둥 좌굴 - 반드시 빠르게 정답을 정확하게 도출하자 (3) | 2025.10.13 |
| 가상 변위의 법칙과 적용 -2023년 7급 국가직 예시 (18) | 2025.10.09 |