가상변위의 법칙, 이렇게 이해하면 쉽다
가상변위의 법칙 -Principle of Virtual Work은
구조역학에서 “외력과 내부력이 평형을 이룰 때, 아주 작은 가상의 변위를 주면 외부일과 내부일의 합이 0이 된다”
는 원리를 말한다.
1. 개념부터 간단히 정리하자
가상의 변위 즉,virtual displacement란
실제로 구조물이 움직이는 변위가 아니라,
“만약 이 구조물이 아주 조금 움직인다면?” 하고
가정하는 가상의 미소한 변위를 뜻한다.
이때 구조물이 평형 상태라면
그 작은 변위에 의한 외부의 일(외력 × 변위)과
내부의 일(내력 × 변위)은 서로 같아야 한다.
즉,
$ \text{외부일} = \text{내부일} $
또는
$ \sum (P_i \delta_i) = \sum (\sigma_j \varepsilon_j V_j) $
이 관계가 바로 가상변위의 법칙 - Principle of Virtual Work 이다.
2. “일의 평형”이라는 관점으로 보기
가상변위의 법칙은 힘의 평형을
일의 평형 ,work equilibrium 으로 바꿔 표현한 것이다.
힘의 평형식은 다음과 같다.
$ \sum F = 0, \quad \sum M = 0 $
하지만, 가상변위의 법칙은
‘힘이 평형이면, 가상의 변위에 대한 일도 평형이다’라고 바꾼 것이다.
즉,
$ \sum (F_i \times \delta_i) = 0 $
이 식이 바로 ‘힘의 평형’을 ‘일의 형태’로 표현한 것이다.
3. 한 줄로 요약하면
“평형 상태에서 아주 작은 변위를 줄 때, 외력이 한 일과 내부력이 한 일이 서로 같다.”
4. 예를 들어보자
스프링에 하중이 작용할 때도 이 법칙이 성립한다.
- 외부일 : $ P \times \delta $
- 내부일 : $ \frac{1}{2} k \delta^2 $ (스프링이 변형되며 내부적으로 저장한 에너지)
평형 시점에서는
$ P \times \delta = \frac{1}{2} k \delta^2 $
이때 $ P = k \delta $, 즉 후크의 법칙이 자연스럽게 나온다.
결국 후크의 법칙도 가상변위의 법칙에서 출발한다고 볼 수 있다.
5. 실전 적용 Ⅰ -2023년 7급 응용역학 9번

빠른 풀이 방법 :
① 50 kN 작용 지점에서의 처짐 $\delta$
$$\delta = \frac{50}{\frac{EA}{6}\times\sin^2(30^\circ)\times2+\frac{EA}{3}}=
\frac{50}{\frac{EA}{6}\times\frac{5}{2}}=\frac{3}{500}$$
② AD의 변형률
$$\epsilon_{AD}=\frac{\delta\times\sin(30^\circ)}{6}=\frac{1}{2000}$$
빠른 풀이의 이해를 위해 가상변위의 법칙을 활용하면 아래와 같습니다.


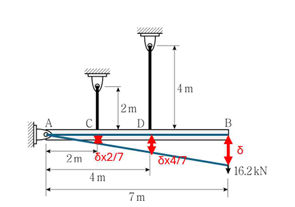
5. 실전 적용 Ⅱ -2023년 7급 응용역학 9번

빠른 풀이 방법 :
① 16.2 kN 작용 지점에서의 처짐 $\delta$
$$\delta=\frac{16.2}{\frac{EA}{2}\times(\frac{2}{7})^2+\frac{EA}{4}\times(\frac{4}{7})^2}=\frac{16.2}{(\frac{2}{49}+\frac{4}{49})\times(EA)}=\frac{16.2}{\frac{6}{49}\times210\times3}=\frac{21}{100}$$
빠른 풀이의 이해를 위해 가상변위의 법칙을 활용하면 아래와 같습니다.

'응용역학-구조역학 필수 이론' 카테고리의 다른 글
| 스프링의 직렬 연결과 병렬 연결 (2) | 2025.10.26 |
|---|---|
| EA가 무한할 때의 자유도와 종속 자유도 (0) | 2025.10.15 |
| 구조물의 자유도 (Degree of Freedom, DOF) (0) | 2025.10.15 |
| 강체 기둥 좌굴 - 반드시 빠르게 정답을 정확하게 도출하자 (3) | 2025.10.13 |
| 2012년 구조역학 5급 공채 문제를 통해서 보는 변위법 (0) | 2025.10.09 |