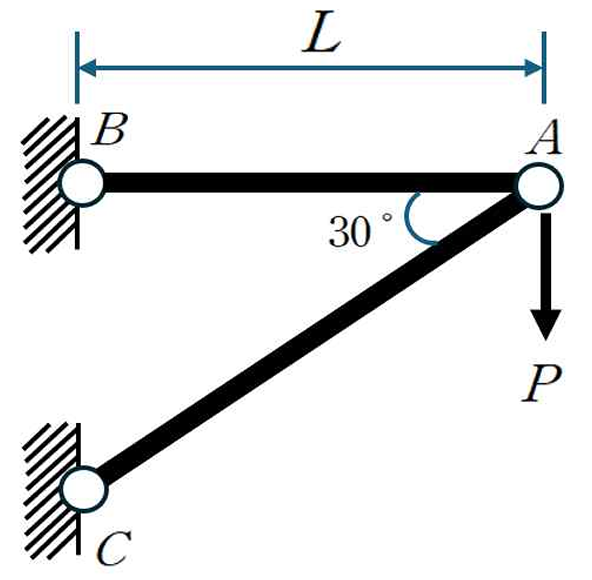
1. 개요구독자분께서 축부재 문제에 대해 질문을 주셔서, 단순히 풀이만 제시하는 데 그치지 않고 자유도 관점까지 확장하여 조금 더 깊게 해석해보려고 합니다.이전에 구독자 대상 라이브 강의에서 축부재의 자유도 산정에 대해 설명드린 적이 있는데, 이번에 질문을 주신 분도 당시 라이브를 보셨던 분이셨습니다. 그 내용을 바탕으로 보면, 위 구조물은 2자유도 시스템으로 해석할 수 있습니다. B와 C 절점은 수평 및 수직 방향 변위가 구속되어 있는 반면, A 절점은 수평·수직 방향으로 변위가 가능하기 때문입니다.저는 이전 포스팅에서 단자유도(자유도=1) 구조물에 대해 가상변위의 법칙을 적용하여 매우 쉽고 빠르게 문제를 푸는 방법을 소개한 바 있습니다. 그 과정에서 변위가 ‘제곱꼴’로 나타나는 이유 또한 가상변위의 ..