[응용역학/스프링 충격] 충격계수 빠른 풀이 vs. 공식 없이 풀기
이번 문제는 다음과 같습니다.
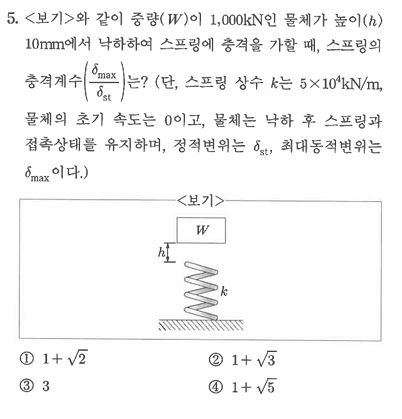
중량 ($W=1{,}000\ \mathrm{kN})인 물체가 높이 (h=10\ \mathrm{mm}$)에서 낙하하여 스프링에 충격을 가할 때, 스프링의 충격계수 ($\delta_{\max}/\delta_{st}$)는 얼마인가?
(단, 스프링 상수 ($k=5\times10^{4}\ \mathrm{kN/m}$), 정적변위는 ($\delta_{st}$), 최대동적변위는 ($\delta_{\max}$).)
1. 충격계수를 암기하고 있을 때 (빠른 풀이)
이 상황의 표준 공식은 다음과 같습니다.
$$
\frac{\delta_{\max}}{\delta_{st}} = 1 + \sqrt{1 + \frac{2h}{\delta_{st}}}
$$
여기서
$$
\delta_{st} = \frac{W}{k}
$$
계산
- ($\delta_{st} = \tfrac{1000}{5\times10^{4}} = 0.02\ \mathrm{m} = 20\ \mathrm{mm}$)
- ($\tfrac{2h}{\delta_{st}} = \tfrac{2 \times 10}{20} = 1$)
따라서
$$
\frac{\delta_{\max}}{\delta_{st}} = 1 + \sqrt{1+1} = 1 + \sqrt{2}
$$
👉 정답: ($1+\sqrt{2}$)
2. 충격계수를 암기하지 않아도 풀기 (에너지 보존법)
공식을 모른다고 해도, 에너지 보존식을 세우면 됩니다.
$$
W(h+\delta_{\max}) = \tfrac{1}{2}k\delta_{\max}^{2}
$$
여기서 ($\delta_{st} = \tfrac{W}{k}$)를 대입하면
$$
\delta_{st}(h+\delta_{\max}) = \tfrac{1}{2}\delta_{\max}^{2}
$$
양변을 ($\delta_{st}^{2}$)로 나누고, ($X = \tfrac{\delta_{\max}}{\delta_{st}}$)로 치환하면
$$
\frac{h}{\delta_{st}} + \frac{\delta_{\max}}{\delta_{st}}
= \tfrac{1}{2}\left(\frac{\delta_{\max}}{\delta_{st}}\right)^{2}
$$
즉,
$$
X^{2} - 2X - 2\frac{h}{\delta_{st}} = 0
$$
수치 대입
- ($\tfrac{h}{\delta_{st}} = \tfrac{10}{20} = 0.5$)
따라서
$$
X^{2} - 2X - 1 = 0
$$
해는
$$
X = 1 \pm \sqrt{1+1} = 1 \pm \sqrt{2}
$$
여기서 (X>0)이므로
$$
X = 1 + \sqrt{2}
$$
결론
- 암기법: 공식만 기억하면 10초 컷
- 비암기법: 에너지 보존 → 2차방정식 유도 → 같은 답
- 최종 정답:
👉 ($\dfrac{\delta_{\max}}{\delta_{st}} = 1+\sqrt{2}$)
'2024년 7급 9급 시험 > 2024년 7급 공무원 서울시' 카테고리의 다른 글
| 2024년 7급 서울시 응용역학 풀이 (“어려워 보여도 기본으로 끝낸다”) (2) | 2025.10.04 |
|---|---|
| 2024년 서울시 7급 응용역학 6번 (쉬운 풀이 와 처짐각법 비교) (0) | 2025.10.04 |
| 2024년 서울시 7급 응용역학 6번 (전단 중심 쉽게 풀자!) (0) | 2025.10.02 |
| 2024년 서울시 7급 응용역학 12번 (매우 쉬운 풀이) (0) | 2025.10.01 |