
1. 개요
(1) 온도에 따른 변형량
온도 변화가 있는 축부재(Bar) 문제는 7급·9급 응용역학에서 매우 자주 등장하는 전형적인 유형입니다.
사실 복잡하게 생각하실 필요는 없습니다.
온도가 상승하면 축부재는 늘어나고,
온도가 하강하면 축부재는 줄어든다.
이 기본 원리를 이해하고 있으면 충분합니다.
온도 변화로 인한 자유 변형량은 다음과 같이 표현됩니다.
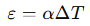
따라서 변형량은

이 됩니다.
하지만 7급·9급 시험에서는 보통 여기에서 멈추지 않고,
양단 구속 상태를 함께 고려하도록 출제됩니다.
(2) 양단 구속 시
온도가 상승하여 부재가 늘어나려 할 때,
양단이 고정되어 있으면 늘어남이 억제되면서 압축력이 발생하게 됩니다.
반대로 온도가 하강하여 부재가 줄어들려 할 때,
양단 구속 때문에 인장력이 생기게 됩니다.
이때 발생하는 내부력(축력)은 다음과 같이 구할 수 있습니다.

즉, 온도 변화에 의한 축력은 길이와 무관하게
재료의 강성(EA)과 온도 변화량(αΔT)에 의해 결정됩니다.
(3) 시험에 자주 출제되는 방식
7급·9급 응용역학에서는 거의 예외 없이
온도가 상승하는 경우(ΔT > 0) 를 다루며,
그에 따른 압축력, 부재력 분배, 직렬·병렬 스프링 치환 등이 함께 묻히는 형태의 문항이 자주 출제됩니다.
온도 문제는 개념만 정확히 이해하면
항상 같은 흐름으로 풀리는 매우 효율적인 점수 확보 구간이므로 꼭 정리해 두시는 것을 추천드립니다.
2. 문제 풀이

(1) 온도 상승치 산정
d 만큼 변형량이 생겨 천장에 닿으려면 다음과 같이 공식이 성립합니다.

따라서 이때의 온도상승치는 다음과 같습니다.
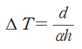
(2) 추가 온도 상승
온도 상승치의 2배가 증가했다고 했으므로 ΔT 만큼 상승되어 양단 구속이 된 후
추가 ΔT의 온도 상승이 생겨 부재력 (압축력)이 생겼다고 해석되어야 합니다.
이때의 압축력은 다음과 같습니다.

압축 응력은 압축력에 단면적을 나눈 것과 같습니다
따라서 다음과 같이 서술 할 수 있습니다.

따라서 답은 ② 입니다.
3. (참고) 온도에 따른 효과를 등가 절점하중으로 치환
축부재의 변형은 힘에 의한 변형과 온도에 의한 변형 두개의 합으로 표현 할 수 있습니다.
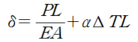
이때 양단 구속조건으로 하여 고정단 하중을 분석해보면 등가 절점하중으로 환산 할 수 있습니다.
δ=0 일때 (양단 구속)으로 하여 P에 대해 풀어보면 다음과 같이 표현 할 수 있습니다.

이에 대한 Fixed End Force 를 살펴보면 다음과 같습니다.

따라서 등가 절점하중은 Fixed Eend Force와 크기는 같고 부호는 반대방향으로 정리할 수 있습니다.

이는 축부재가 ΔT 만큼 온도가 증가하며 벽을 밀어내는 힘과 동일합니다.
4. 마무리하며
축부재에서의 온도 변화나 제작 오차는
재료역학 전반에서 매우 자주 등장하는 대표적인 유형입니다.
따라서 건축·토목 관련 각종 시험에서도 반복적으로 출제되는 주제입니다.
이러한 문제들은 변형률(strain) 관점에서 사고하면 훨씬 간단해집니다.
“얼마나 늘어나고, 얼마나 줄어드는가?”를 기준으로 접근하면
구조가 복잡하더라도 해석이 자연스럽게 정리됩니다.
또한 간단하게 소개드린 등가 절점하중(Equivalent Nodal Load) 개념 역시
축부재 해석시 알게 되면 매우 유용합니다.
이 개념은 앞으로 다룰 부정정 축부재 문제를 풀 때도
매우 강력한 도구로 활용해보도록 하겠습니다.
지속적으로 따라오시면 축부재·온도·제작오차·부정정 해석이 모두
하나의 흐름으로 자연스럽게 연결되는 것을 느끼실 수 있을 것입니다.
'재미있는 문제- 쉬운풀이 > 축 부재 (axial member)' 카테고리의 다른 글
| 2009년 국가직 7급 15번 문제 (자중+축부재 유형) (0) | 2025.12.11 |
|---|---|
| 2015년 서울시 7급 12번 (축부재의 에너지 산정+심화 개념) (0) | 2025.12.01 |
| 2023년 국가직 7급 9번과 2025년 서울시 7급 14번 비교 (Truss) (0) | 2025.11.08 |
| 2017년 7급 국가직 응용역학 12번 - 온도 변화 트러스를 대하는 자세 (0) | 2025.10.25 |
| 2024년 7급 군무원 응용역학 5번 (적분법/ 등가면적법/ 직관적 사고법) (0) | 2025.10.05 |