[응용역학] 원형 테이퍼 막대의 축변형 – 적분법, 등가단면법, 직관적 사고법 비교
아래의 예제를 통해 세 가지 접근법(적분법, 등가단면법, 직관적 사고법)을 비교해보겠습니다.
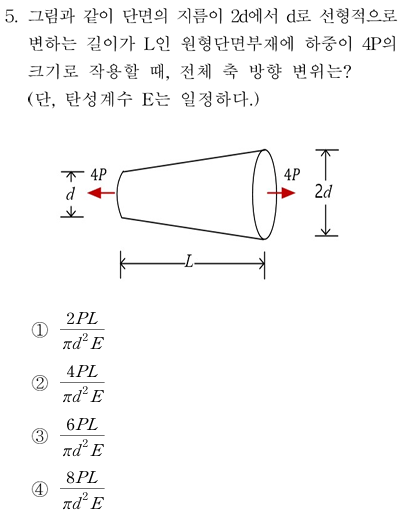
문제
지름이 $2d$에서 $d$로 선형적으로 변하는 원형 단면 부재(길이 $L$)에
축방향 하중 $4P$가 작용할 때,
전체 축방향 변위는 얼마인가?
(단, 탄성계수 $E$는 일정하다.)
1. 적분법
가장 기본적인 접근법은 변위의 정의식부터 출발한다.
$$
\delta = \int_0^L \frac{N(x)}{E A(x)} dx
$$
이때 축력 $N(x)$는 일정하므로 $N(x) = 4P$이다.
지름이 선형적으로 변하므로
$$
D(x) = d\left(1 + \frac{x}{L}\right)
$$
따라서 단면적은
$$
A(x) = \frac{\pi}{4} D(x)^2 = \frac{\pi d^2}{4}\left(1 + \frac{x}{L}\right)^2
$$
이를 식에 대입하면
$$
\delta = \int_0^L \frac{4P}{E \cdot \frac{\pi d^2}{4} (1 + \frac{x}{L})^2} dx
= \frac{16P}{\pi d^2 E} \int_0^L \frac{dx}{(1 + \frac{x}{L})^2}
$$
치환 $u = 1 + \frac{x}{L}$, $du = dx/L$을 적용하면
$$
\delta = \frac{16PL}{\pi d^2 E} \int_1^2 u^{-2} du
= \frac{16PL}{\pi d^2 E}\left(1 - \frac{1}{2}\right)
= \frac{8PL}{\pi d^2 E}
$$
정답
$$
\delta = \frac{8PL}{\pi d^2 E}
$$
적분법은 원리를 그대로 적용한 방법으로 가장 정확하지만, 계산량이 많아 시간이 오래 걸린다.
2. 등가단면법
테이퍼진 단면을 일정한 단면으로 바꾸어 계산하는 방법이다.
즉, 실제 단면 대신 동일한 변형을 주는 가상의 일정 단면적 $A_{eq}$를 도입한다.
정의식은 다음과 같다.
$$
\frac{1}{A_{eq}} = \frac{1}{L} \int_0^L \frac{dx}{A(x)}
$$
지름이 선형적으로 변할 경우 이 적분 결과는 다음과 같이 단순화된다.
$$
A_{eq} = \frac{\pi}{4} d_1 d_2
$$
이는 두 단의 지름을 곱한 값의 기하평균 단면적을 의미한다.
따라서 변위는
$$
\delta = \frac{N L}{E A_{eq}} = \frac{4P L}{E \cdot \frac{\pi}{4} d_1 d_2}
= \frac{8PL}{\pi d^2 E}
$$
결과적으로 적분법과 완전히 동일한 값을 얻을 수 있다.
단 한 줄로 정답을 도출할 수 있어 실전에서 가장 효율적이다.
3. 직관적 사고법
적분을 수행하지 않고, 극단적인 두 경우를 비교하여 변형의 대략적 크기를 추정하는 방법이다.
단면이 전부 $2d$일 때
$$
\delta_{2d} = \frac{4PL}{(\pi /4)(2d)^2 E} = \frac{4PL}{\pi d^2 E}
$$
단면이 전부 $d$일 때
$$
\delta_d = \frac{16PL}{\pi d^2 E} = 4\delta_{2d}
$$
따라서 실제 변형은 다음 범위 안에 존재한다.
$$
\frac{4PL}{\pi d^2 E} < \delta < \frac{16PL}{\pi d^2 E}
$$
단면이 작은 쪽에서 변형이 집중되므로,
단순한 평균(약 10)보다 작은 쪽(즉, 큰 변형 쪽)에 더 가깝게 위치한다.
4와 16 사이에서 약 1:2 비율로 내분된 값, 즉 8 정도가 가장 합리적이다.
결과적으로 직관적인 판단만으로도 정답 8에 근접한 값을 예상할 수 있다.
'재미있는 문제- 쉬운풀이 > 축 부재 (axial member)' 카테고리의 다른 글
| 2015년 서울시 7급 12번 (축부재의 에너지 산정+심화 개념) (0) | 2025.12.01 |
|---|---|
| 2015년 7급 서울시 응용역학 3번 (온도 상승 + 축부재) (0) | 2025.11.19 |
| 2023년 국가직 7급 9번과 2025년 서울시 7급 14번 비교 (Truss) (0) | 2025.11.08 |
| 2017년 7급 국가직 응용역학 12번 - 온도 변화 트러스를 대하는 자세 (0) | 2025.10.25 |
| 2025년 7급 응용역학 가형 24번 풀이 (0) | 2025.09.27 |