
1.개요
위 문제를 보면, 절점에서의 회전각이나 중앙 대칭축 상의 처짐을 묻지 않고, 중심선(5 m)에서 1 m 떨어진 6 m 지점이라는 다소 의외의 위치에서의 처짐을 요구하고 있습니다.
처짐을 구하는 방법은 여러 가지가 있습니다.
임의의 점에서 처짐을 구해야 할 때, 여러분은 어떤 방법을 가장 자주 사용하시나요?
손계산 기준으로는 공액보법을 가장 많이 활용하는 편이고, 단위하중법 역시 매우 널리 쓰이는 방법입니다. 다만 보 구조물에서 단위하중법의 경우, 손적분 과정에서 계산량이 늘어날 수 있다는 점은 감안해야 합니다.
이 외에도 다양한 해석 방법이 존재하지만, 이 문제에서는 출제자가 의도적으로 배치한 흥미로운 장치가 하나 눈에 띕니다.
바로 해당 부재가 ‘순수 휨(pure bending) 상태’에 놓여 있다는 점입니다.
이 특성을 잘 활용하면, 기존의 정석적인 절차와는 다른 조금 더 직관적이고 재미있는 방법으로도 문제를 풀 수 있습니다.
이제 그 접근법을 하나씩 살펴보겠습니다.
2. 순수 휨 (Pure Bending)에서의 처짐 (순수 기하학의 활용)
(1) 기본 이론
우선 보부재에서 곡률은 다음과 같이 표현될 수 있습니다.
κ 를 곡률이라 할때,
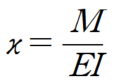
위의 문제에서는 M이 전 구간에서 10kNm로 일정합니다.
따라서 곡률은

한편, 곡률은 처짐곡선의 2계 미분꼴입니다.
따라서
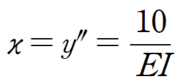
따라서 처짐 곡선은 완벽한 2차 포물선 공식이 됩니다.

(2) 문제 풀이에 활용
순수모멘트 보부재는 처짐곡선이 2차 포물선이라고 한다면
다음과 같이 쓸 수 있습니다. (δ는 가운데지점 (x=5)에서의 처짐)
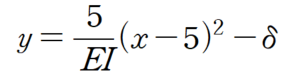
위의 식을 쓸수 있는 논리는 다음과 같습니다.
① 2번 적분하였으므로 x^2 의 계수는 곡률에 해당
② x=5에서 대칭축
③ x=5 대입했을 때 처짐값 (-δ)
이제 δ를 찾으면 되는데 이는 매우 쉽게 유도 됩니다.
x=0 지점 (지점 A)에서의 처짐이 0이기 때문에
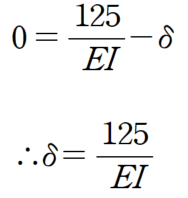
따라서 처짐곡선식은 다음과 같습니다.
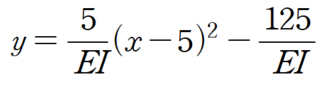
x=6 인 지점의 처짐을 산정하면 다음과 같습니다.

따라서 답은 ③번이 됩니다.
3. 공액보법 (Conjugate Beam Method)
M/EI 도를 그려보면 10/EI가 일정하게 그려집니다.
공액보법풀이는 이를 등분포하중으로 치환하여 x=6지점의 모멘트를 산정하여 처짐을 산정하는 방식입니다.
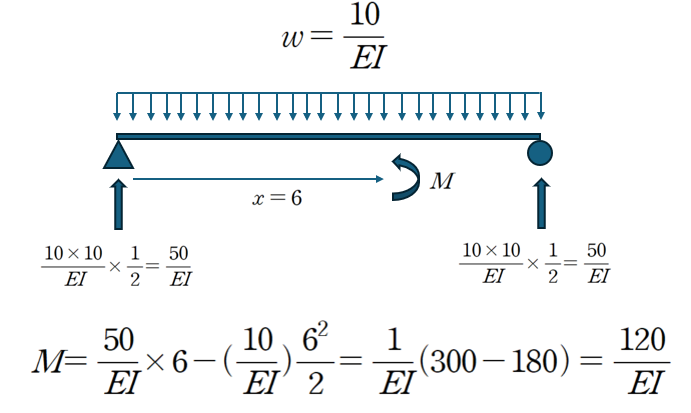
공액보의 모멘트는 처짐에 해당하므로 답은 동일하게 ③이 됩니다.
4.단위 하중법 (Principle of Virtual Force : Unit Force Method)
우선 주어진 구조물의 모멘트선도 (BMD)를 그려보면

10으로 일정하게 됩니다.
이제 구하고자 하는 지점에 단위하중 1을 가하게 되면


4.마무리하며
이중적분법, 공액보법, 단위하중법은 모두 일반적으로 처짐을 구할 때 널리 사용되는 방법들입니다.
하지만 순수 휨(pure bending) 상태에서는 조금 다른 접근이 가능합니다.
순수 휨 상태에서는 곡률이 일정하므로, 처짐 형상이 2차 포물선을 이룬다는 특징이 있습니다.
이 점을 활용하면, 굳이 이중적분을 끝까지 수행하지 않고도 처짐의 2차 포물선 방정식을 직접 설정하여 문제를 해결할 수 있습니다. 이번 풀이에서는 바로 이 아이디어를 이용한 방법을 소개해 보았습니다.
즉, 순수 휨 상태에서는 처짐 문제가 훨씬 단순화될 수 있으며, 이 사실만 알고 있어도 문제 접근 방식이 크게 달라질 수 있습니다.
한편, 공액보법과 단위하중법은 일반적인 처짐 문제를 풀기에 매우 강력한 도구이지만, 하중 조건이 조금만 복잡해져도 손계산량이 급격히 증가한다는 단점이 있습니다.
특히 시험 환경에서는 이 계산 부담이 풀이 전략에 큰 영향을 미치기도 합니다.
이와 관련하여, 예전 포스팅에서는 공액보법에 등가절점하중 개념을 결합하여 계산량을 크게 줄이는 방법을 소개한 바 있습니다.
이 방법은 시중 문제집이나 일반 강의에서는 거의 다루지 않는 방식으로, 현재로서는 이 블로그에서만 정리되어 있는 내용입니다.
다양한 풀이 방법을 접해 두면 단순히 “푸는 것”을 넘어,
어떤 상황에서 어떤 방법이 가장 효율적인지 판단하는 눈을 기를 수 있습니다.
이번 문제가 그런 관점에서 한 번쯤 생각해 볼 계기가 되었으면 합니다.
'재미있는 문제- 쉬운풀이 > 정정 보의 곡률, 처짐' 카테고리의 다른 글
| 2018년 서울시 2차 7급 4번 (삼각함수 처짐곡선의 재미있는 특성) (0) | 2026.02.13 |
|---|---|
| 2018년 1차 서울시 7급 17번 (온도를 공액보법으로 확장 적용) (0) | 2026.02.09 |
| 2007년 7급 국가직 응용역학 19번 (처짐을 빠르게 구하는 사고) (0) | 2025.11.30 |
| 2015년 7급 서울시 응용역학 7번 (보부재의 온도 변화 처리) (0) | 2025.11.16 |
| 2025년 7급 응용역학 가형 22번 풀이 (공액보법으로 푸는 방법) (0) | 2025.11.11 |