
1. 개요
문제를 해결하는데 헷갈릴수 있는 개념을 집고, 문제를 효율적으로 풀어 나가는 사고에 대해 소개하겠습니다.
위의 문제를 보면 AC 부재가 pin–pin 조건으로 되어 있습니다.
그렇다면 자연스럽게 다음 질문이 생깁니다.
“C점에서 처짐이 발생하면, AC 부재는 그 처짐을 휨강성으로 저항할 수 있을까?”
정답은 저항할 수 없습니다.
그 이유는 매우 단순합니다.
✔ Pin–Pin 부재는 처짐에 대해 휨저항을 만들 수 없다
어떤 부재가 처짐을 ‘저항’하려면 반드시 양 끝단에서 모멘트가 발생해야 합니다.
즉, 처짐이 일어날 때 끝단이 회전을 저항해야 휨모멘트가 생기고, 그 모멘트가 처짐을 억제하는 역할을 하게 됩니다.
그러나 pin–pin 부재는:
- 양 끝단 모두 모멘트 = 0
- 회전이 완전히 자유
- 따라서 처짐에 대해 어떠한 저항도 제공하지 못함
즉, C점이 아래로 내려가더라도 AC 부재는
‘그냥 회전하며 따라 내려가는 것’ 뿐이며
이 부재의 EI(휨강성)는 사실상 처짐 저항에 기여하지 못합니다.
아래의 포스팅도 읽어보시는 것을 추천합니다.
https://oreostructure.tistory.com/75
단순보의 지점 처짐에 대한 질문 (구독자 질문)
1.개요구독자분들께 실질적인 도움이 되고자,질문 중 많은 분들이 공통적으로 궁금해하실 만한 내용은별도 포스팅으로 정리해 드리는 방식으로 운영해 보려고 합니다.이번 글은 한 구독자 분께
oreostructure.com
✔ 만약 A 지점이 고정단이었다면?
이 경우는 전혀 달라집니다.
A가 고정단이면:
- A단에서 회전이 구속됨 → 모멘트 발생
- C점의 처짐에 대해 휨강성으로 저항
- 결과적으로 부정정 구조물이 됨
- C점 처짐은 “캔틸레버 AC + 캔틸레버 CB”의 병렬 연결 구조처럼 치환 가능
즉, “A–C–B 전체가 처짐을 공동으로 저항하는 스프링 네트워크”가 됩니다.
그러나 주어진 문제는 pin–pin 구조이므로
이러한 병렬연결 개념은 전혀 적용되지 않습니다.
✔ 그럼 어떻게 접근해야 할까? (시험장에서의 효율 전략)
이 문제의 핵심은 다음 한 문장으로 요약됩니다.
“처짐을 알고 싶은 지점(D점)에 하중을 직접 몰아주자.”
그렇게 되면 필요 없는 부분들을 걷어 내고 우리가 아는 가장 기본 구조인 캔틸레버로 치환할 수 있습니다.
하중을 이동하면 모멘트 평형에 변화가 생기면 안되기 때문에 이에 따라 새로 생기는 모멘트도 고려해줘야 합니다.
이와 같은 유의사항만 생각한다면 문제를 쉽게 해결할 수 있습니다.
2. 문제풀이
(1) 자유 물체도
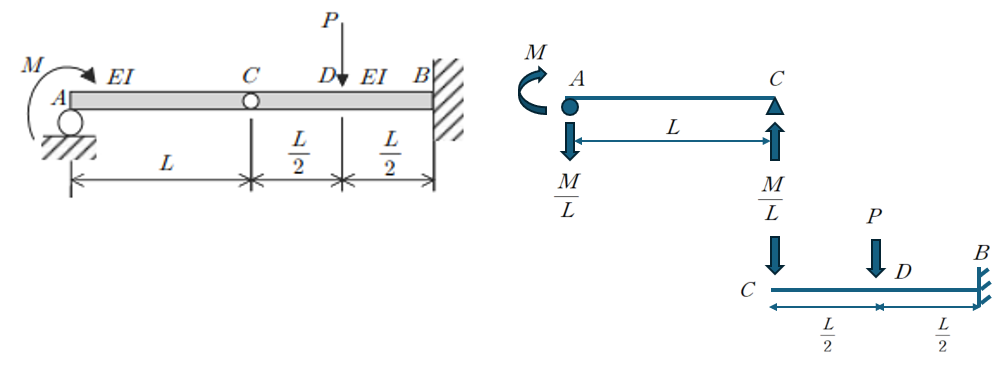
위 그림에서 AC 부재는 C점에 내부 힌지가 존재하여 pin–pin 조건을 만족합니다.
따라서 AC 부재는 단순보와 동일한 방식으로 구조해석을 해도 무방합니다.
이때 중요한 점은, C점의 반력은 부재 CB가 C점을 누르는 하중으로 그대로 작용한다는 사실입니다.
즉, AC 부재는 단지 전달 경로 역할을 할 뿐, C점의 처짐을 저항하는 휨강성을 제공하지 않습니다.
따라서 문제에서 구하고자 하는 D지점의 처짐을 계산할 때에는
굳이 AC 부재 전체를 고려할 필요가 없습니다.
(2) 하중의 이동
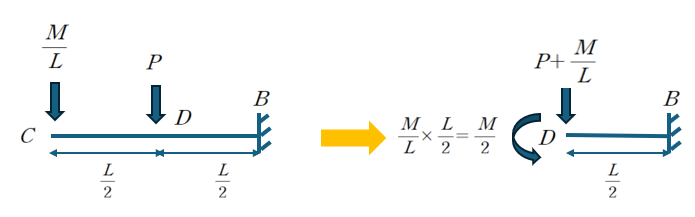
C점의 M/L이라는 하중을 이동시 고려해야 할 것이 있습니다.
그것은 이동 경로대로 거리를 고려하여 모멘트를 고려해줘야 한다는 점입니다.
이 원리에 대해 이해하려면 자유물체도를 그려보면 좋습니다.
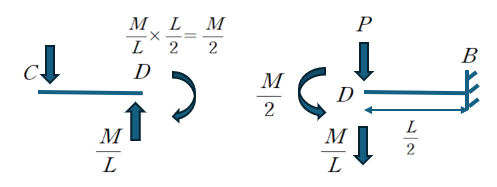
CD 부재를 따로 분리하여 봤을 때, 모멘트가 D지점에 작용하며,
이에 대한 반작용으로 DE 부재의 D에 크기는 같고 반대방향의 모멘트가 작용하는 것으로 해석할 수 있기 때문입니다.
이제 우리는 가장 간단한 캔틸레버 문제의 자유단에 하중이 작용할 시 처짐을 산정하는 문제로 치환하였습니다.
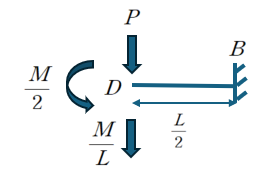
따라서 암기하고 있는 캔틸레버 자유단 처짐공식을 활용하면 처짐을 다음과 같이 산정할 수 있습니다.
(3) 처짐 산정
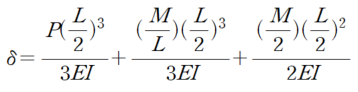
처짐 δ를 산정하기 위해 연산을 끝까지 하지 말고 보기를 최대한 활용해 주십시오.
δ는 P와 M의 항으로 나뉘어 있습니다.
P에 대한 부분만 떼어내서 보면 PL^3/24EI 입니다.
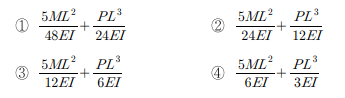
보기 중 이를 충족하는 것은 ①번 뿐입니다.
3. 마무리하며
처짐 문제를 풀 때 가장 중요한 것은 빠르고 효율적인 사고 논리를 구축하는 것입니다.
개요에서 말씀드렸듯이, 먼저 구조를 보자마자
병렬·직렬 스프링 구조로 치환할 수 있는가를 판단해보는 것이 좋습니다.
이 접근이 가능하다면 연산량이 급격히 줄어들고, 구조물의 거동을 훨씬 직관적으로 이해할 수 있습니다.
다음으로 고려해야 할 전략은 하중을 한 지점에 몰아넣기(Equivalent Load Concentration) 입니다.
즉, 구조물을 우리가 이미 알고 있는 가장 단순한 형태—캔틸레버·단순보·스프링—로 변환하여
그 구조에서 처짐을 계산하는 방식입니다.
처짐을 구하는 방법은 매우 다양합니다.
대표적으로
- 단위하중법(가상일의 원리),
- 모멘트 면적법,
- 공액보법,
- 처짐각법 등
정석적인 방법들이 존재합니다.
하지만 7급·9급 응용역학 시험 환경을 생각해 보면,
계산기 없이 제한된 시간 안에 손으로 계산해야 합니다.
따라서 복잡한 적분이 여러 번 등장하는 방식은 실전에서 비효율적일 수밖에 없습니다.
시험장에서 중요한 것은
“정석적으로 모든 단계를 거쳐 푸는가”가 아니라,
“구조를 단순화하여 최소한의 연산으로 정확한 답을 도출할 수 있는가”입니다.
결국 실전에서 고득점을 좌우하는 것은
공식 암기보다도 구조물을 단순화시키는 전략적 사고이며,
이러한 사고법을 꾸준히 연습하셔야 시간 절약과 정답률 향상이라는 두 가지 목표를 동시에 만족시킬 수 있습니다.
'재미있는 문제- 쉬운풀이 > 정정 보의 곡률, 처짐' 카테고리의 다른 글
| 2018년 1차 서울시 7급 17번 (온도를 공액보법으로 확장 적용) (0) | 2026.02.09 |
|---|---|
| 2017년 서울시 7급 응용역학 1번 (순수휨 정정보의 처짐을 산정하는 여러방법) (0) | 2025.12.22 |
| 2015년 7급 서울시 응용역학 7번 (보부재의 온도 변화 처리) (0) | 2025.11.16 |
| 2025년 7급 응용역학 가형 22번 풀이 (공액보법으로 푸는 방법) (0) | 2025.11.11 |
| 공액보법의 응용으로 쉽게 풀기 (2025년 서울시 7급 13번) (0) | 2025.11.07 |