
1.개요
처짐 문제에서 손계산으로 가장 많이 활용되는 방법은 아마도 공액보법일 것입니다.
모든 처짐 해석은 결국 같은 뿌리, 즉 모멘트에 의한 곡률에서 출발하지만
곡률을 이중적분하는 방식은 시험장에서 짧은 시간 내 손계산으로 처리하기에 부담이 큽니다.
반면 공액보법은 모멘트에 의한 곡률 분포를 하중으로 치환하여 다루기 때문에
훨씬 직관적이고 적용이 수월한 장점이 있습니다.
이러한 맥락에서 위의 문제를 다시 살펴보겠습니다.
이 문제에는 외력 하중이 전혀 존재하지 않고,
오직 온도 변화만 주어져 있습니다.
여기서 많은 수험생들이 놓치기 쉬운, 하지만 반드시 먼저 확인해야 할 질문이 하나 있습니다.
이 구조물은 정정 구조물인가, 부정정 구조물인가?
A지점이 고정단이고 B지점이 지지되어 있으므로 겉보기에는 1차 부정정처럼 보일 수 있습니다.
하지만 A점에서는 전단력이 해제(shear release) 되어 있습니다.
이 조건을 고려하면, 해당 구조물은 정정 구조물이 됩니다.
이 부분이 매우 중요합니다.
이전 포스팅에서도 여러 차례 강조했듯이, 정정 구조물에서의 온도 변화는 구속을 만들지 않습니다.
즉, 온도 변화로 인해 추가적인 구속력이나 내력은 발생하지 않습니다.
따라서 이 문제에서 B지점의 회전각을 구하기 위해서는 힘의 평형이나 부정정 해석이 아니라
온도 변화로 인해 발생하는 순수한 기하학적 변형만 고려하면 됩니다.
이를 기하학적으로 접근하면 자연스럽게 온도 변화에 따른 곡률을 이중적분하는 방식이 떠오를 수 있습니다.
하지만 이 과정을 손으로 수행하는 것은 시간도 오래 걸리고 비효율적입니다.
바로 이 지점에서 같은 원리를 뿌리로 삼고 있는 공액보법을 활용할 수 있습니다.
모멘트에 의한 곡률 다이어그램을 온도 변화에 따른 곡률 다이어그램으로 치환하면,
문제는 매우 간단해지고 계산 또한 빠르게 끝낼 수 있습니다.
결국 중요한 것은 어떤 공식을 더 많이 아느냐가 아니라,
구조물의 성격을 먼저 판단하고 가장 단순한 물리적 원리로 문제를 바라보는 시각입니다.
2.문제풀이
(1) 온도 분포에 따른 곡률 산정

(2) 보 구조물의 곡률분포

(3) B지점의 회전각 산정
회전각이 0인 Fixed roller 지점에서 곡률이 누적된 값을 산정하면 B지점의 회전각에 해당하게 됩니다.
따라서 다음과 같이 산정됩니다.
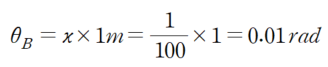
따라서 답은 ②번이 됩니다.
3.문제풀이를 넘어서
(1) A지점의 처짐 산정
이때는 B지점의 회전각을 활용하시면 됩니다.
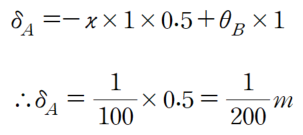
즉, 하향으로 1/200m 만큼 내려가게 됩니다.
(2) C지점의 처짐 산정
이때도 B지점의 회전각을 활용하시면 됩니다.

즉, 상향으로 0.0048m 만큼 올라가게 됩니다.
(3) 곡률이 일정 → 2차 함수를 활용하는 전략
"곡률이 일정하면 2차 함수다"라는 점을 활용하여 문제를 푸시면 매우 효율적으로 문제를 해결할 수도 있습니다.
꼭지점은 회전각이 0인 지점에서 발생하므로 지점 A가 꼭지점에 해당합니다.
참고로, AB구간과 BC구간은 동일 곡률을 갖고 있으며
B에서의 회전각과 변위가 적합조건에 의해 동일하기 때문에 동일 처짐곡선을 갖는 것으로 보아도 됩니다.
2차함수 꼴인 처짐곡선식을 산정하면 다음과 같습니다.

이를 통해 위에서 산정한 값들에 대해 검증해보겠습니다.
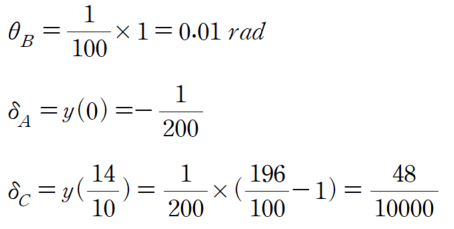
간편하게 결과 값이 동일하게 나오는 것을 검산할 수 있습니다.
4.마무리하며
이로써 온도 효과를 공액보법에 확대 적용하는 방법을 살펴보았습니다.
문제에서 요구한 B지점의 회전각은 실제로 30초 이내에 충분히 해결 가능한 문제였습니다.
하지만 기출을 볼 때 여기서 멈추면 안 됩니다.
한 단계 더 나아가 “그렇다면 처짐은 어떻게 구할 수 있는가?”까지 이어서 생각해 보아야 합니다.
그리고 이 과정에서 방금 산정한 B지점의 회전각이 어떻게 활용되는지를 함께 살펴보았습니다.
곡률이 일정한 경우에는
처짐곡선을 2차 함수 형태로 일반화하여 접근하는 전략도 매우 유효합니다.
반드시 공액보법만을 고집할 필요는 없으며,
처짐곡선식을 빠르게 유도할 수 있다면
회전각과 처짐을 모두 손쉽게 도출할 수 있다는 점도 함께 확인하였습니다.
기출문제를 풀 때에도
항상 하나의 풀이에만 매달리기보다,
더 쉽고 빠르게 접근할 수 있는 다른 방법은 없는지를 고민해 보시기 바랍니다.
이와 같은 연습을 반복하다 보면
자연스럽게 본인만의 노하우와 풀이 스킬이 축적되고,
그 스킬은 단순 암기가 아니라
어떤 문제에도 흔들리지 않는 확장 가능한 실력으로 자리 잡게 될 것입니다.
'재미있는 문제- 쉬운풀이 > 정정 보의 곡률, 처짐' 카테고리의 다른 글
| 2017년 서울시 7급 응용역학 1번 (순수휨 정정보의 처짐을 산정하는 여러방법) (0) | 2025.12.22 |
|---|---|
| 2007년 7급 국가직 응용역학 19번 (처짐을 빠르게 구하는 사고) (0) | 2025.11.30 |
| 2015년 7급 서울시 응용역학 7번 (보부재의 온도 변화 처리) (0) | 2025.11.16 |
| 2025년 7급 응용역학 가형 22번 풀이 (공액보법으로 푸는 방법) (0) | 2025.11.11 |
| 공액보법의 응용으로 쉽게 풀기 (2025년 서울시 7급 13번) (0) | 2025.11.07 |