
1.개요
[참고] 2026년 국가직 7급 근로감독 산업안전 응용역학 풀이
2026년 국가직 근로감독 산업안전 7급 응용역학 풀이 (전략적인 접근)
바로 풀린다” 리스트 (문제당 30초 내외)1 (단면의 기본), 2 (포아송비 활용의 기본), 3(평면응력의 기본), 4(정정 1차원 축부재 기본)5(평형방정식), 6(평형방정식), 7(SFD, BMD의 기본), 8(응력의 기본)9
oreostructure.com
이전에 2026년 7급 근로감독 산업안전 응용역학 문제를 풀이하면서, 23번 문항이 상대적으로 난도가 높은 문제에 해당한다고 언급한 바 있습니다. 당시 저는 해당 문항을 변위일치법을 기반으로 접근하여 풀이하였습니다.
변위일치법은 일반적으로 부정정 구조물 해석에서 자주 활용되는 풀이 기법입니다. 실제로 인터넷에 공개된 과거 7급·9급 응용역학 해설들을 살펴보면, 부정정 구조물 문제의 상당수가 응력법을 기반으로 한 변위일치 방식으로 해결되고 있음을 확인할 수 있습니다.
물론 변위일치법은 매우 강력한 풀이 방법임에 틀림없습니다. 다만 특정 조건에서는 등가 절점하중과 변위법을 함께 사용하는 접근이 훨씬 직관적이고 강력해지는 경우도 존재합니다.
저는 과거에 다음과 같은 이야기를 한 적이 있습니다.
부정정 차수가 높을수록, 그리고 구조물의 자유도가 낮을수록 변위법이 강력해지며, 이와 반대의 경우에는 응력법이 더 효율적인 선택이 될 수 있다는 점입니다.
이러한 경향은 대부분의 경우 기술사 시험이나 기술고시 시험에서도 잘 들어맞는 판단 기준이며, 공학용 계산기라는 강력한 도구가 허용되는 환경에서도 크게 달라지지 않습니다.
앞서 언급한 문제를 변위일치법으로 풀이한 내용은, 위에 링크해 둔 2026년 7급 응용역학 풀이 포스팅을 통해 참고하시기 바랍니다.
이제부터는 동일한 문제를 대상으로, 변위법을 기반으로 한 다른 관점의 풀이 방식을 소개해 드리도록 하겠습니다.
2.문제풀이
보 DE는 단일 스프링으로 치환할 수 있습니다. 중앙부의 처짐 공식을 활용해 보면 스프링 치환은 간단하게 산정됩니다.


따라서 캔틸레버 보 구조물 AB에 집중하중과 모멘트가 동시에 작용하는 구조물로 변환할 수 있습니다.
모멘트 25.5kN을 처짐을 동일하게 하는 집중하중으로 (즉, 등가절점하중 으로) 추가 변환할 수 있습니다.
이는 25.5 kN를 반대로 Carry Over한 후 이 두 모멘트의 합을 보의 길이 방향으로 나누어 집중하중으로 변환하면 됩니다.
그렇게 되면 아래와 같이 51/4kN의 추가 집중하중이 발생하게 됩니다.
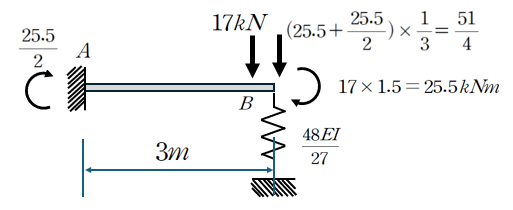
따라서 아래와 같이 더 간편화 할 수 있습니다.

스프링과 캔틸레버가 병렬연결임을 활용하여 B의 처짐을 산정할 수 있습니다.

이제 처짐값을 구했으니 처짐각 공식을 통해 A점의 모멘트를 산정할 수 있습니다.
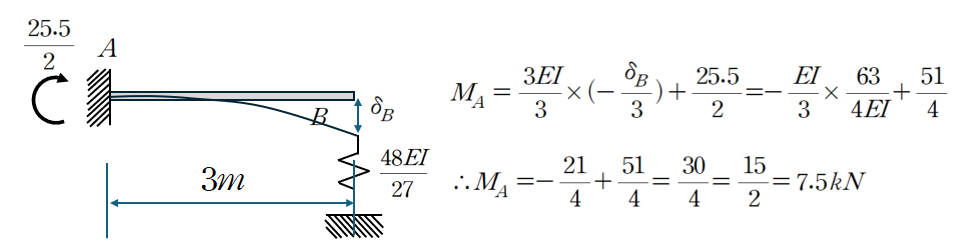
3. 마무리하며
이번 글에서는 일반적으로 응력법을 기반으로 한 변위일치법으로 풀이되는 문제를, 구조물의 강성 개념을 중심으로 어떻게 변위법의 관점에서 해석할 수 있는지를 소개해 보았습니다.
변위법을 통한 접근 역시 생각보다 복잡하지 않으며, 구조를 한 번 정리해 두면 오히려 계산 과정이 단순해지는 장점도 있습니다. 응용역학·구조역학이라는 학문에서 응력법과 변위법은 각각 독립된 기법이 아니라, 서로를 보완하는 두 개의 큰 축이라고 생각합니다. 어느 한쪽에만 치우치기보다는, 두 방법 모두를 단단히 다져 두었을 때 비로소 문제에 대한 폭넓은 응용이 가능해집니다.
이번 글에서는 변위법을 활용하여 2026년 7급 시험에서 상대적으로 까다롭게 느껴질 수 있는 문제를 직접 다뤄보았습니다. 풀이 과정을 참고하시되 단순히 따라가는 데서 그치지 마시고, 각 단계가 어떤 의미를 갖는지 스스로 정리해 보시기 바랍니다. 이를 통해 변위법 역시 여러분만의 하나의 강력한 Tool로 체득하시길 바랍니다.
'재미있는 문제- 쉬운풀이 > 부정정 보의 해석' 카테고리의 다른 글
| 2014년 서울시 7급 15번 (기출 회독 학습의 의미) (0) | 2026.02.11 |
|---|---|
| 2018년 2차 서울시 7급 11번 (필요한 자유도만 취해서 빠르게 풀이) (0) | 2026.02.05 |
| 2019년 7급 국가직 응용역학 10번 (부정정 보 처짐의 쉬운 풀이) (0) | 2026.01.20 |
| 2009년 7급 국가직 응용역학 5번 문제 (변위 기반의 생각) (0) | 2025.12.06 |
| 2015년 7급 서울시 응용역학 10번 (해답을 넘은 해설 : 영향선과 FEM) (0) | 2025.11.26 |