
1.개요
부정정 구조물의 해석을 보면, 사람마다 선호하는 풀이 방식이 조금씩 다릅니다.
예를 들어 구조기술사나 계산기를 적극적으로 활용해 온 분들은
최소일의 원리나 가상일의 법칙을 이용한 적분 기반 풀이를 자연스럽게 선호합니다.
기술사 문제의 전형적인 풀이 구조가
평형방정식 → 부정정 차수 판별 → 최소일·가상일을 통한 해석
의 순서를 따르기 때문입니다.
하지만 7급·9급 시험처럼 손계산만으로 풀어야 하는 시험에서는
적분 풀이가 오히려 가장 불리한 전략이 됩니다.
- 제곱, 세제곱 연산에서 계산 실수가 나기 쉽고
- 더하고 빼는 과정까지 반복되면 시간이 급격히 늘어나며
- 시험장에서 한 번 실수하면 만회가 어렵습니다.
많은 분들이 “더 집중하자, 눈 크게 뜨고 풀자”라고 반성하지만
계산 실수는 집중한다고 사라지는 문제가 아닙니다.
연산 자체를 최소화하는 구조로 접근해야 실수가 줄어듭니다.
그래서 저는 7급·9급 시험에서는
‘변위를 기반으로 하는 접근(변위법적 사고)’이 훨씬 효과적이라고 강조드리고 싶습니다.
핵심 Insight
문제에서 C점의 수직 반력이 0이라는 것은 무엇을 의미할까요?
C점에 롤러가 있다고 상상하는 것이 아니라, 자유단이라 가정하였을 때, 그 지점의 처짐이 0이라는 의미입니다.
즉, 구조물의 경계조건이
“C점 처짐 = 0”
이라는 단 한 줄로 표현됩니다.
이 조건만 이해하면 문제는 더 이상 부정정 문제가 아니라
정정 구조물의 해석으로 바뀝니다.
결국 해야 하는 일은 단 하나,
“C점의 처짐이 0이 되도록 하는
MB 와 MC의 비율을 찾으라.”
이것만 구하면 됩니다.
여기에는 1차 부정정력을 따지고
최소일·적분을 해야 하는 과정이 전혀 필요 없습니다.
2. 문제풀이
개요에서 설명한 논리대로 풀이를 하면 문제는 매우 간단하게 풀립니다.

그림을 통해 위의 공식이 어떻게 유도되었는지 설명하겠습니다.
(1) 필수 암기 공식 (캔틸레버의 처짐)
7급, 9급을 준비하시는 수험생 분들은 자유단에 모멘트가 가해졌을 때, 회전각과 처짐 공식은 암기하고 계셔야만 합니다.

이는 모멘트 면적법에 의해 쉽게 유도 될 수 있습니다.
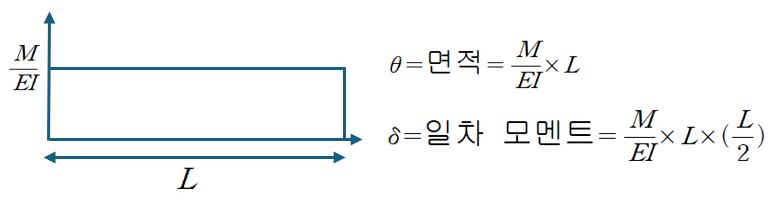
(2) MB에 의한 C점의 처짐
중앙부의 B지점에서 MB가 작용했을때의 처짐에 대해 알아보겠습니다.

기본 공식에 의거하여 δ1과 θ1은 다음과 같습니다. (윗방향과 반시계방향을 -부호로 설정하였습니다,)
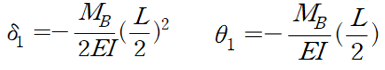
BC구간은 모멘트값이 0이므로 굽힘이 없이 일직선으로 거동합니다.
따라서 δ2는 각도 × 길이로 처짐이 간단하게 산정됩니다.
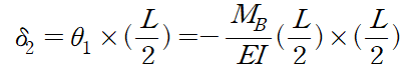
따라서 C점의 처짐은 다음과 같이 산정됩니다.
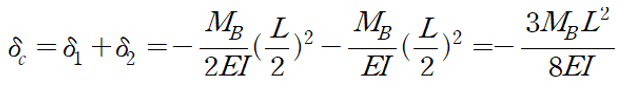
(3) MC에 의한 C점의 처짐
C점의 처짐은 캔틸레버의 기본 처짐 공식으로 쉽게 산정됩니다.

(4) MB와 MC로 인한 δc 의 중첩
선형탄성에서는 중첩의 원리가 성립하므로 각각 두가지 Case의 δc를 더해줍니다.
C점의 총 변위는 0이다라는 공식을 세우면 마무리 됩니다.

처짐 자체가 0이므로 밑에 롤러가 있어도 롤러에 가해지는 하중자체가 부재하게 되므로 반력 또한 0이 됩니다.
3. 마무리하며
일차 부정정으로 다소 복잡하게 풀이될 것만 같던 문제풀이를
관점을 변위로 이동시켜 간단한 캔틸레버보의 처짐 문제로 치환하였습니다.
이번 문제를 통해 다시 한 번 확인할 수 있는 사실은,
7급·9급 응용역학은 손계산 시험이기 때문에
“얼마나 복잡하게 풀 수 있는가”가 아니라
“얼마나 단순하게 줄여서 풀 수 있는가”가 실력의 핵심입니다.
앞으로 문제를 보실 때도
부정정 구조물을 만나면 먼저 계산부터 시작하지 마시고,
변위의 관점에서 문제를 단순하게 할 수 있는가 고민하시게 되면
실력도 향상되고 연산의 양도 줄게 되여 시험장에서 정답률 상승과 시간절약을 모두 취할 수 있습니다.
'재미있는 문제- 쉬운풀이 > 부정정 보의 해석' 카테고리의 다른 글
| 2026년 7급 근로감독 산업안전 응용역학 23번 (변위법적인 쉬운 접근) (0) | 2026.01.26 |
|---|---|
| 2019년 7급 국가직 응용역학 10번 (부정정 보 처짐의 쉬운 풀이) (0) | 2026.01.20 |
| 2015년 7급 서울시 응용역학 10번 (해답을 넘은 해설 : 영향선과 FEM) (0) | 2025.11.26 |
| 2015년 7급 서울시 응용역학 5번 (부정보의 지점침하) (2) | 2025.11.16 |
| 가상 변위의 법칙으로 강성도 산정 및 등가하중으로 처짐 구하기 (2024년 서울시 7급 16번) (0) | 2025.11.03 |