
1. 개요
자중이 작용하는 축부재의 해석은 일반적인 집중하중 축부재 문제와는 성격이 확연히 다릅니다. 축부재의 자중은 부재 전체에 걸쳐 연속적으로 분포하며, 높이가 올라갈수록 그 아래에 누적된 부재의 무게가 증가하게 됩니다. 따라서 축력은 아래에서 위로 갈수록 선형적으로 증가하는 형태를 띠게 됩니다. 이는 하나의 절점에 집중하중이 작용하는 전형적인 축부재 문제와 비교했을 때 분명한 차이점입니다.

이번 포스팅에서는 이러한 자중의 효과를 해석하는 두 가지 접근법을 소개하려고 합니다.
첫째는 시중 문제집에서 흔히 다루는 고전적(Classic) 접근법으로, 연속 분포하중을 고려하여 축력을 적분해 구하는 방식입니다.
둘째는 제가 블로그에서 자주 강조하는 방식으로, 자중을 등가 절점하중으로 치환하여 빠르게 해석하는 방법입니다. 이 방식은 연산량을 크게 줄일 수 있어 실제 시험장에서 매우 강력한 전략이 될 수 있습니다.
두 가지 풀이를 함께 비교해보며 자중이 있는 축부재 해석의 본질을 정확하게 이해하고, 시험에서는 어떤 방식이 가장 효율적인지 판단할 수 있도록 도와드리겠습니다.
2. 문제풀이 (고전적 방법)
(1) A 구조물의 처짐
임의의 x 만큼 떨어진 지점의 자유물체도를 그리고 변형량을 산정하면 다음과 같습니다.
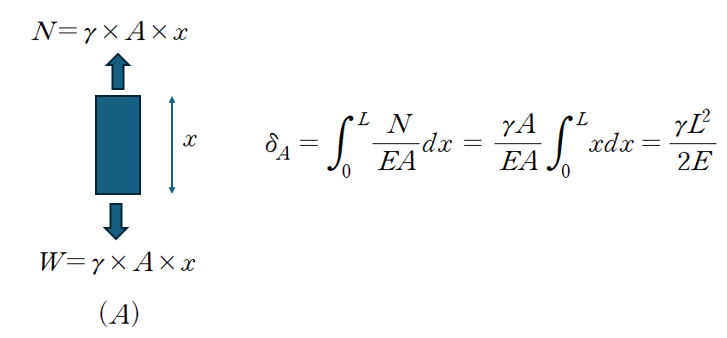
(2) B 구조물의 처짐
2 구간에 대해 자유물체도를 그려 분석하면 아래의 그림과 같습니다.

위의 적분식을 풀어보면 다음과 같습니다.

(3) δA / δB 산정
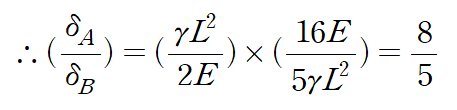
따라서 답은 ③이 됩니다.
3. 문제풀이 (등가절점하중)

자중처럼 선형분포의 분포 축하중을 나타내는 경우
양 끝절점의 등가하중은 위 그림과 같이 삼각형의 총 하중을 절점 끝에 작용하는 것과 동일합니다.
따라서 (A)의 경우

그리고 (B)의 경우

따라서 끝단의 처짐은 다음과 같습니다.

따라서
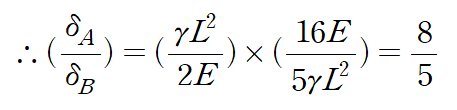
답은 동일하게 나옵니다.
4. 마무리하며
고전적인 방식으로 적분을 활용해 자중에 의한 축력을 계산해도 되지만, 사실 시험 관점에서 보면 등가 절점하중으로 치환하여 단순한 집중하중 문제로 바꾸어 푸는 방법이 훨씬 효율적입니다. 이번 포스팅을 따라가 보시면, 후자의 방식이 전자보다 연산량이 얼마나 크게 줄어드는지 직접 체감하실 수 있을 것입니다.
적분 기반의 고전적 해석은 개념을 정확히 이해하기 위해 반드시 알아야 하는 접근법입니다. 특히 구조해석의 기초를 쌓는 과정에서 축력의 분포 형태가 왜 선형이 되는지, 왜 적분을 통해 얻는지가 중요한 학습 요소입니다. 하지만 실제 시험 환경에서는 부담스러운 손적분보다 등가 절점하중을 활용한 치환 접근법이 압도적으로 유리합니다. 연산속도 면에서도 빠르고, 무엇보다 계산 실수 가능성이 크게 줄어듭니다.
다만 이러한 등가 절점하중 치환 기법은 시중 교재에서 자세히 다루지 않는 경우가 많습니다. 제가 블로그에서 반복적으로 소개하는 이유도 바로 여기에 있습니다. 꾸준히 포스팅을 따라오시면, 적분 대신 단번에 절점하중으로 바꿔버리는 강력한 도구를 자연스럽게 체화하실 수 있을 것입니다.
'재미있는 문제- 쉬운풀이 > 축 부재 (axial member)' 카테고리의 다른 글
| 2018년 응용역학개론 국가직 9급 14번 (축부재의 응력법과 변위법) (0) | 2026.02.26 |
|---|---|
| 2010년 지방직 7급 응용역학 16번 (직관적 + 빠른 풀이) (0) | 2026.01.30 |
| 2015년 서울시 7급 12번 (축부재의 에너지 산정+심화 개념) (0) | 2025.12.01 |
| 2015년 7급 서울시 응용역학 3번 (온도 상승 + 축부재) (0) | 2025.11.19 |
| 2023년 국가직 7급 9번과 2025년 서울시 7급 14번 비교 (Truss) (0) | 2025.11.08 |