
1. 개요
모멘트 분배법을 활용한 풀이도 충분히 가능하지만,
https://oreostructure.tistory.com/98
2024년 7급 국가직 응용역학 22번 (모멘트 분배법 풀이, 수정된 강성도)
1. 개요이번 문제는 2024년 국가직 7급 22번으로 출제되었던, 좌우 대칭 프레임의 절대 최대 휨모멘트를 구하는 문항입니다.문제에서 “좌우 대칭인 라멘 구조물”이라는 문구를 굳이 언급한 이유
oreostructure.com
이 문제의 그림을 자세히 보면 출제자가 의도적으로 제공한 장치가 하나 존재합니다.
바로 A점에서의 수평반력 P/8 입니다.
해당 구조물은 전체적으로 보면 폐합 구조이기 때문에, 형식적으로는 3차 부정정 구조물에 해당합니다.
그러나 좌우 대칭 조건을 활용하여 모델링하면, 구조의 자유도가 줄어들어 2차 부정정 구조물로 단순화할 수 있습니다.
여기서 중요한 포인트는,
문제에서 이미 A점의 수평반력 P/8을 명시적으로 주었다는 점입니다.
수평반력은 원래 해석 과정에서 구해야 할 미지 반력에 해당하는데,
이 값이 이미 주어졌다는 것은 곧 미지력 하나가 제거되었다는 의미입니다.
즉,
- 대칭 조건을 적용하여 2차 부정정 구조로 단순화한 상태에서
- 추가로 수평반력까지 주어졌기 때문에
결과적으로 이 구조물은 1차 부정정 구조물처럼 해석할 수 있는 상태가 됩니다.
이와 같은 관점에서 접근하면,
굳이 계산량이 많은 모멘트 분배법을 사용하지 않더라도
출제자가 의도한 사고 흐름을 따라 훨씬 간결하게 문제를 해결할 수 있습니다.
2. 문제풀이
(1) 대칭 모델링 & 부정정 차수 산정
아래 그림과 같이 Fixed Roller 지점을 E 점이라 한다면 해당 절점에 수평력과 모멘트는 미지력이 됩니다.
E가 자유단이라고 한다면 ABE는 전체적으로 캔틸레버 정정구조물과 같은 형태를 띄게 되기 때문입니다.
따라서 기존 3차 부정정 구조물에서 대칭으로 인한 Fixed Roller 모델링 시 부정정 차수는 3차에서 2차로 줄어들게 됩니다.

이때 문제에서는 A지점의 수평력을 주어졌기 때문에 E점의 수평반력 HE가 결정됩니다.

따라서 이 문제는 부정정 차수가 하나 줄어 1차 부정정 처럼 풀이가 가능해 집니다.
(2) 자유물체도

Fixed Roller로 인해 Sway가 발생하지 않으므로 B는 Sway에 저항하는 롤러지점이 있는 것처럼 거동합니다.
(참고로 이전 Frame 문제풀이에서 Sway가 있을 경우 캔틸레버 취급 했던 것을 기억하고 비교하시면 좋습니다.)
(3) 적합방정식
① 기둥 AB에서 지점 B의 회전각
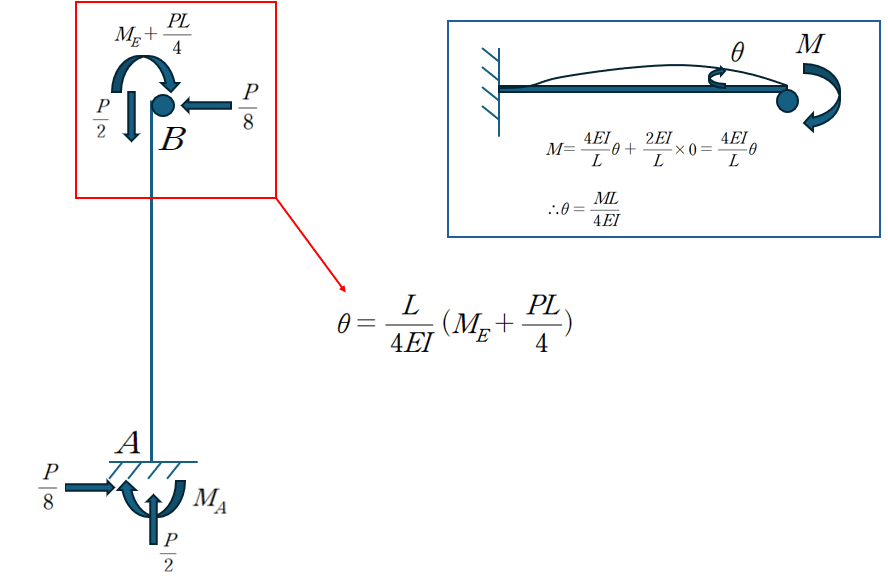
② 보 BE에서 지점 B의 회전각

③ 적합방정식 ( 기둥 AB에서 지점 B의 회전각 = 보 BE에서 지점 B의 회전각 )

(4) 모멘트 산정
① 기둥 AB에서 B 절점 모멘트, A 지점 모멘트 산정

② 보 AE에서 B 절점 모멘트, E 지점 모멘트 산정

③ A와 B 중 최대 모멘트 산정
구조물에서 발생하는 절대 최대 모멘트는 하중이 작용하는 BC의 중앙점 (E점)이지만
문제에서 물어보는 AB 부재에서의 절대 최대 모멘트는 B점에서 발생하며 크기는 PL/12입니다.
답은 ②번으로 동일하게 나옵니다.
3. 마무리하며
문제를 살펴보면 1차 부정정 구조물처럼 해석할 수 있는 형태이기 때문에, 자연스럽게 변위일치법으로 접근해야겠다는 판단을 할 수 있었습니다.
만약 이러한 관점으로 접근하지 않았다면, A점에 대한 변위 적합방정식을 추가로 세워 수평반력을 직접 산정해야 했을 것입니다. 그러나 해당 반력은 이미 문제 조건으로 주어져 있으므로, 불필요한 연산을 생략하고 비교적 간단하게 문제에 접근할 수 있었습니다. 이로써 본 문제에 대해 모멘트 분배법과 변위일치법, 두 가지 풀이 방식을 모두 제시할 수 있었습니다.
한편, 제 블로그를 꾸준히 보신 분들이라면 다음과 같은 의문이 자연스럽게 떠오를 수 있을 것입니다.
“Fixed roller 부재에 대한 수정된 강성도를 모멘트 분배법에서 활용했는데,
이 개념을 변위일치법이나 더 나아가 처짐각법에도 적용하면 더 간단해지지 않을까?”
이에 대한 답은 그렇다입니다.
Fixed roller에 작용하는 하중 PPP를 등가 절점하중으로 치환한 뒤 해석하면, 변위일치나 처짐각법에서도 매우 간단한 형태로 문제를 풀 수 있습니다.
이와 같은 접근 방법에 대해서는 다음 포스팅에서 자세히 다루도록 하겠습니다.
'재미있는 문제- 쉬운풀이 > Frame 구조물' 카테고리의 다른 글
| 2020년 지방직 7급 응용역학 9번 (가장 단순한 풀이) (0) | 2025.12.17 |
|---|---|
| 2024년 7급 국가직 응용역학 22번 (한줄풀이로 단순화 하기) (0) | 2025.12.15 |
| 2009년 국가직 7급 16번 문제 (변위일치로 풀기) (0) | 2025.12.10 |
| 2009년 국가직 7급 문제 9번 (구조물 처짐에 대한 올바른 관점) (0) | 2025.12.09 |
| 2007년 7급 국가직 응용역학 4번 (변형도에 대한 직관적인 풀이) (0) | 2025.11.28 |