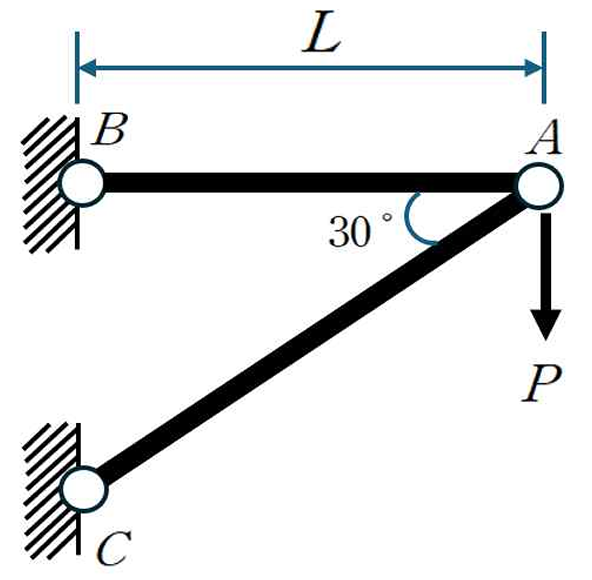
1월 14일, 구독자 분을 위한 라이브 문제 풀이를 진행하였습니다.참가자는 한 분이었으며, 사실상 개인 과외에 준하는 형태로 최대한 밀도 있게 진행하였습니다.참여하신 분은 이미 어느정도 기본적인 응용역학 개념과 시중 문제 풀이에는 조금 익숙하신 분이었고,단순한 정답 풀이를 넘어 실력 업그레이드와 새로운 시각, 전략적인 인사이트를 얻고자 참여해 주셨습니다.이번 라이브에서는 2025년 서울시 7급 응용역학 1번부터 10번까지를 다루며,각 문항마다 “기존 풀이와는 다른 관점”을 중심으로 설명을 이어갔습니다.문항별 주요 내용 정리1번 문항비틀림 문제를 단순 공식 대입으로 보지 않고,축부재 단자유도 구조와의 유사성, 극좌표계의 개념 소개,나아가 탄소성 비틀림의 개념까지 확장하여 설명하였습니다.또한 부정정 비틀림 ..