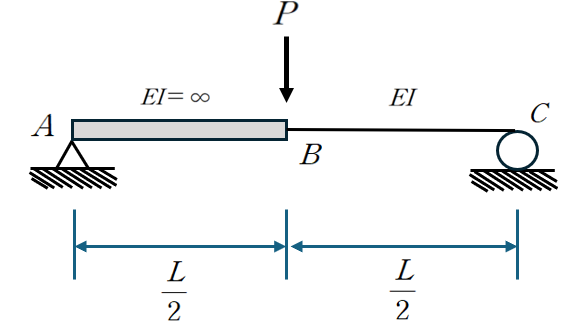
1.개요한 구독자 분께서“EI 강체(EI → ∞)가 오히려 문제를 더 쉽게 만든다”는 제 의견에 대해 깊은 인상을 받으셨다고 하며,여러 가지 EI 강체가 포함된 문제들을 직접 시도해 보신 후 위 문제에 대해 질문을 주셨습니다.해당 구독자 분은 역학 자체에 흥미가 있고기존 풀이와는 다른 접근법을 탐구하는 데 관심이 많으며현재 서울시 7급을 준비 중인 수험생이라고 밝혀 주셨습니다. 이번 글에서는 그분의 질문을 바탕으로,위 구조물을 변위법의 관점에서 해석하여 B점의 수직 처짐을 구하는 과정을 살펴보겠습니다. 조금 개념적인 이야기가 될 수 있지만, 핵심은 다음과 같습니다.위 구조물은 C점의 회전 자유도를 무시할 수 있는 조건(EI 강체) 이 주어져 있으므로,이를 통해 수정된 강성도(modified stiffne..