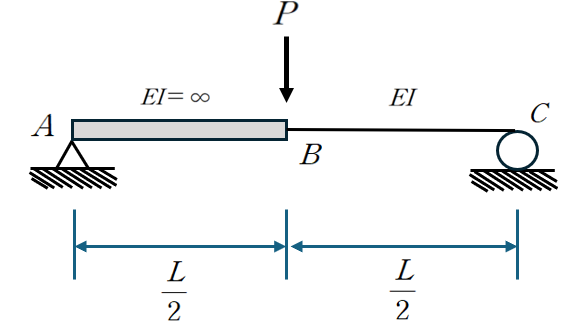
바로 풀린다” 리스트 (문제당 30초 내외)1 (합력, 평형방정식_바리뇽의 정리), 2 (SFD, BMD 기본), 4(케이블 정리 기본)6(영향선활용 부반력 찾기), 9 (스프링 직렬 병렬 연결), 10 (모멘트 면적 - 사다리꼴 면적 구하기), 11(응력의 비율 : 물성치가 약분되어서 간단해짐), 12(모멘트 분배법)13(소성상태에서 평형방정식), 14 (2차원 응력 변형률, 포아송비 활용), 17번 (스프링직렬연결, 변위일치), 18 (유연도 활용한 변위일치)19번 ( 공액보법의 활용, 20 (트러스 절점법 및 부재 강성도 활용)“시간이 걸리지만 풀만하다” 리스트 혹은 "낯선 유형"5 (트러스 0부재 찾기 : 부재가 조금 많아서 실수할수도 있기 때문에 쉬운것 부터 건들고 오는것이 바람직)7 (스프링 ..