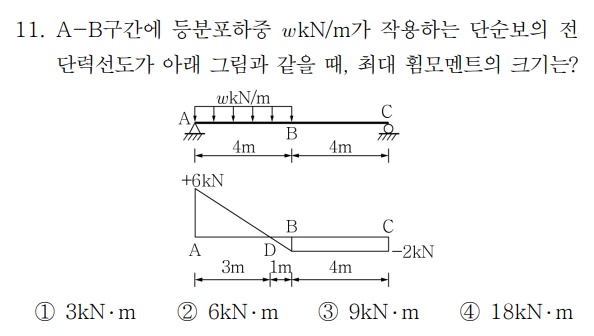
1. 개요일반적으로 분포하중이 작용하는 보에서 최대 휨모멘트를 찾고자 할 때는휨모멘트 식 M(x) 을 미분하여 0이 되는 지점을 찾습니다. 한편 휨모멘트와 전단력은 다음과 같은 관계를 갖습니다.따라서 “전단력이 0이 되는 지점 = 휨모멘트가 최대(또는 최소)가 되는 지점”입니다.시험에서도 최대모멘트를 묻는다면 자연스럽게 전단력이 0인 위치를 찾는 흐름으로 접근하게 됩니다.이번 문제에서는 출제자가 이러한 과정을 쉽게 하라고전단력도(Shear Force Diagram, SFD) 를 직접 제시했습니다.덕분에 반력을 따로 계산할 필요 없이,SFD에서 지점에 해당하는 값을 그대로 읽어 반력을 바로 구할 수 있습니다.이 부분에서 출제자의 배려가 느껴집니다.그렇다면 등분포하중 은 어떻게 찾아낼 수 있을까요?전단력도에..