Insight 구조&응용역학

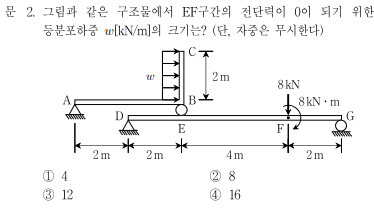
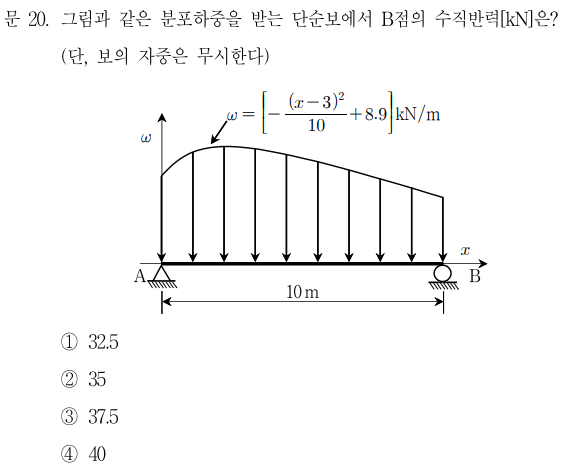
1. 스프링의 직렬 연결① 구조적 의미두 개 이상의 스프링이 한 줄로 연결되어 한 점에서 다음 점으로 순차적으로 하중을 전달하는 형태입니다.즉, 모든 스프링에 걸리는 힘은 동일하지만, 변형(변위)은 각 스프링마다 독립적으로 발생합니다.스프링을 여러 개 줄줄이 이어 붙인 모습을 떠올려보세요.마치 침대 매트리스의 스프링을 세로로 한 줄로 쌓아 놓은 모양입니다.이런 상태에서 위에서 누르면,수직 배열된 스프링에 같은 힘이 전달되지만,각 수직 배열된 스프링이 눌리는 정도(변형) 는 다를 수 있습니다.② 자유도 관점각 스프링은 자체적으로 늘어나거나 줄어들 수 있으므로,구조 전체의 자유도는 스프링 수에 따라 증가합니다.예를 들어, 위 그림처럼 고정점–스프링1–스프링2–하중점 형태라면,스프링1과 스프링2의 변형은 독립..

1. 개요보통 이러한 유형의 문제는 단위하중법(Unit Load Method) 을 이용해 푸는 경우가 많습니다.하지만 이번에는 단위하중법 대신 ‘자유도(Degree of Freedom)’ 의 개념으로 구조물을 분석해 봅시다.이 접근법은 계산 과정을 단순화하면서도 문제의 본질을 훨씬 명확하게 파악할 수 있는 강력하고 효율적인 방법입니다.특히 이러한 시각은 2025년 7급 응용역학 24번 문제와 같은 유사 유형을 빠르고 정확하게 해결하는 데 큰 도움이 됩니다.해당 구조물은 정정 트러스(Statically Determinate Truss) 입니다.이유는 구해야 할 부재력이 5개이고, 세울 수 있는 평형방정식 또한 5개이기 때문입니다.여기에 온도 변화가 발생했다는 조건은 매우 의미 있는 조건입니다.왜냐하면 온도..

1. 개요 위의 문제를 다음과 같은 2개 방식으로 풀어보겠습니다① 평형방정식② 가상변위의 법칙난이도는 下 문제이지만 2가지의 측면으로 문제를 바라보는 것이 의미 있어 포스팅을 올립니다. 2. 평형방정식구조물을 다음과 같이 나눠서 볼수 있습니다.구조물 ABC의 모멘트 평형을 통해 A와 B의 반력은 w/2라는 점은 금방 나옵니다.보 DG에서 모멘트 평형을 구해 D 지점의 반력을 산정 후 EF의 전단력이 0이 되려면, 산정된 값이 w/2와 동일해야 합니다.따라서 , 다음과 같이 쓸 수 있습니다.3. 가상변위의 법칙변형도를 그리는데 익숙해지면 kinematic 관계는 정정구조물에 대해서 매우 금방 산정할 수 있습니다.가상변위는 EF 구간 중앙에 shear release를 하여 주었습니다.이때 각 외부일이 한 일..

이번 문제는 세 가지 방법으로 접근해 보겠습니다.① 최소일의 원리② 처짐각법③ 모멘트 면적법세 방법 모두 손계산으로 충분히 풀 수 있는 수준이며,개인적으로는 이 문제에 대해서는 최소일의 원리가 가장 간단하다고 판단합니다.하지만 어떤 분은 모멘트 면적법이 더 직관적이라고 생각하실 수도 있겠죠.즉, 어느 방법이 더 편한지는 다소 주관적인 부분이 있다고 봅니다.또한, 본 문제에서는 EI가 무한대인 구간을 어떻게 다루는가에 대한변위법 관점의 접근도 함께 생각해 보시면 좋겠습니다.이 포스팅이 그 점에서 이해를 확장하는 계기가 되었으면 합니다.1. 최소일의 원리2. 처짐각법강체부(EI가 무한대인 구간)가 δ₁만큼 변위가 생기면, 그 회전각이 곧 EI가 유한한 구간이 시작되는 지점의 초기 기울기 조건이 됩니다.3.모..

B지점 수직반력, 영향선으로 한 줄에 끝내기문제:길이 10 m 단순보에 다음과 같은 분포하중이 작용한다.$$\omega(x) = -\frac{(x-3)^2}{10} + 8.9 ;[\mathrm{kN/m}]$$이때 B지점 수직반력 ( R_B )을 구하여라.(단, 보의 자중은 무시한다.)1. 뮬러–브레슬라우로 영향선 그리기구하고 싶은 값은 B지점의 수직반력 ( R_B ) 이므로B지점의 지지력을 제거하고 위로 단위변위 ( +1 ) 을 주면 그때의 변형형상이 영향선이다.단순보의 영향선은 선형이므로$$y_{\mathrm{IL}}(x) = \frac{x}{L} = \frac{x}{10}, \qquad (0 \le x \le 10)$$가상변위의 법칙(virtual work principle)에 따라,$$R_B = \..

2024년 9급 응용역학개론 기출 풀이 총평2024년 9급 응용역학개론 시험은 전반적으로 기존에 출제되던 유형에서 크게 벗어나지 않았다.기본 개념을 정확히 이해하고 있다면 계산이 복잡하지 않고, 빠르게 풀 수 있는 문제들이 대부분이었다.1. 전반적 경향이번 시험은 기본 원리를 명확히 알고 있는 수험생이라면 큰 어려움 없이 풀 수 있는 수준이었다.공식 암기보다 개념 이해를 중심으로 공부했다면 계산 과정이 거의 필요하지 않은 문제들이 많았다.2. 신유형 문항이번 시험에서 눈에 띄는 새로운 유형은 13번 문제였다.Müller-Breslau의 영향선법을 활용하는 문제로,가상변위의 법칙을 이해하고 있다면 어렵지 않게 해결할 수 있다.거더 하단에 전단 해제(shear release)가 주어졌을 때,위쪽 바닥판의 변..

총평2023 국가직 시험은 계산량이 많지 않았으며, 대부분의 문항을 가상변위의 법칙으로 간단히 정리할 수 있었다.대부분 수험생들이 평형방정식(∑F=0, ∑M=0) 기반의 전통적 풀이에 익숙하지만, 이번 해설에서는 그와 달리 가상변위의 법칙을 활용하여 평형방정식과 비교하는 방식을 취했다.가상변위의 법칙을 사용하면 문제를 한 줄로 정리할 수 있고, 기하학적 관계(kinematic relation) 또한 매우 단순해진다.인터넷상에서 흔히 볼 수 있는 동일한 풀이 대신, 구조역학의 본질적 원리를 이해하는 데 초점을 맞췄다.이 풀이를 따라가면 “힘의 평형”과 “변위의 관계”가 동일한 결과를 내는 이유를 직관적으로 이해할 수 있을 것이다.대부분의 문제는 예상 가능한 boundary 조건 내에서 출제되었으며,비례·반..

총평2024년 7급 국가직 응용역학 시험은 일부 계산을 요구하는 문항이 있었지만, 전반적으로 많은 연산이 필요한 편은 아니었다.7급의 난점은 “문제 자체의 난도”보다 “한정된 시간 안에 손계산으로 정확히 끝내는 것”에 있다.기출은 항상 편안한 의자에 앉아 아이스아메리카를 마시며 공학계산기로 풀며 연습하면 누구나 풀수 있는 난이도의 문제다.따라서 계산기를 활용하며 어리석은 방식으로 문제를 풀지말고, 실전과 같은 조건에서 문제를 어떻게 하면 쉽게 풀 수 있을지를 평상시에 고민하자. 실수를 줄이고 시간을 단축하려면 다음 원칙을 적극 활용하자.대칭이 있으면 반드시 대칭 장치를 쓴다.사칙연산이 길어지면 분수를 활용하고 공통된 것을 묶는다.보기를 최대한 활용한다. 특히 보기의 단위는 큰 힌트가 되는 때가 많다.단면..

구조해석에서 자유도(Degree of Freedom, DOF)는 구조물이 독립적으로 움직일 수 있는 방향의 수를 의미한다.그러나 구조물의 일부 부재가 매우 큰 축강성(EA)을 가질 경우, 일부 자유도는 서로 종속 관계를 이루게 된다.이 글에서는 축강성이 무한할 때 자유도에 어떤 변화가 생기는지, 그리고 종속 자유도가 어떤 의미를 가지는지를 정리한다.1. EA가 무한하다는 뜻축강성은 부재가 축방향 변형을 얼마나 억제하는지를 나타내는 값으로,$$ EA = E \times A $$이다.여기서 $E$는 탄성계수, $A$는 단면적이다.$EA$가 무한대라는 것은 부재가 축방향으로 신장되거나 압축될 수 없다는 뜻이다.즉, 부재의 양 끝단 사이 길이가 절대 변하지 않는 상태이다.$$\delta = \frac{N L}{..

구조물의 자유도 (Degree of Freedom, DOF)구조물 해석에서 자유도(Degree of Freedom, DOF)란구조물이 자유롭게 움직일 수 있는 독립된 방향의 수를 말한다.즉, 구조물이 몇 가지 방식으로 움직일 수 있는지를 나타내는 개념이다.1. 자유도의 기본 개념하나의 절점(Joint)이 자유롭게 움직일 수 있는 방향은 최대 세 가지다.수평 방향 이동 ($x$ 방향) 수직 방향 이동 ($y$ 방향) 회전 ($\theta$ 방향)예를 들어, 한 점이 $x$, $y$ 방향으로 이동할 수 있고 회전도 가능하다면그 절점은 총 3개의 자유도를 가진다.2. 전체 자유도 (Global DOF)Global DOF는 구조물 전체가 가질 수 있는 자유도의 수를 의미한다.예를 들어 절점이 $N$개인 평면..