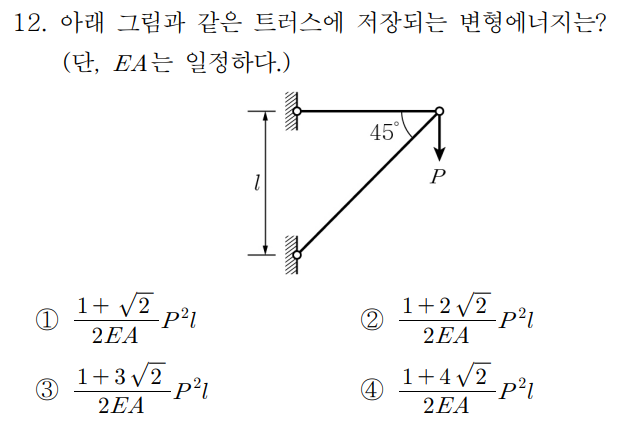
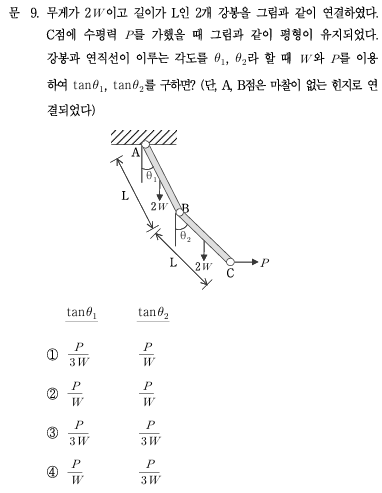
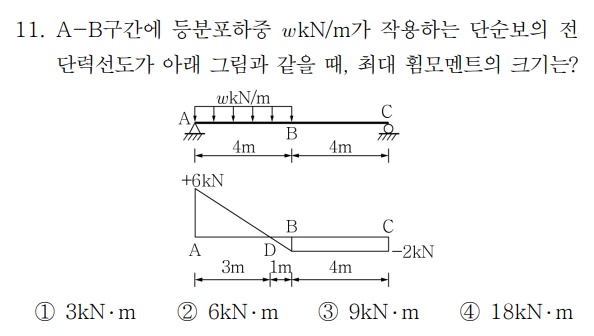
1.개요깔끔하고 아름다운 문제란 어떤 문제일까요?저는 개념에 충실한 문제가 가장 아름다운 문제라고 생각합니다.핵심 개념을 정확히 알고 있다면 자연스럽게 해법이 보이고,반대로 개념이 부족하면 불필요하게 돌아가야 하거나 시간이 크게 걸리는 문제,이런 구조가 바로 “잘 만든 문제”입니다.위 문제는 그런 의미에서 제가 생각하는 아름다운 문제의 전형입니다.왜냐하면,Stiffness(강성)의 정의,병렬 연결의 개념,그리고 직관적인 구조 감각이 세 가지를 정확히 이해하고 있다면,문제는 단숨에 풀립니다.하지만 이 개념들을 놓치고불필요하게 “1차 부정정 구조 해석”에만 집중하게 되면,연산이 늘어나고방향성을 잃기 쉽고결국 비효율적인 풀이에 빠지는 전형적인 상황이 벌어집니다.단순한 개념으로 빠르게 푸는 사람과,기계적 계산으..